Sample Mean
Definition:
The sample mean of a set of ![]() samples from a particular
realization of a stationary stochastic process
samples from a particular
realization of a stationary stochastic process ![]() is defined
as the average of those samples:
is defined
as the average of those samples:
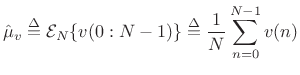 |
(C.17) |
For a stationary stochastic process
| (C.18) |
Next Section:
Variance
Previous Section:
Mean



















