Nonuniform Spectral Resampling
Recall sinc interpolation of a discrete-time signal [270]:
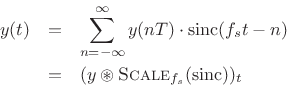
And recall asinc interpolation of a sampled spectrum (§2.5.2):
![\begin{eqnarray*}
X(\omega) &=& \hbox{\sc DTFT}(\hbox{\sc ZeroPad}_{\infty}(\hbox{\sc IDFT}_N(X)))\\
&=& \sum_{k=0}^{N-1}X(\omega_k)\cdot \hbox{asinc}_N(\omega-\omega_k)\\ [5pt]
&=& (X\circledast \hbox{asinc}_N)_\omega,
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1296.png)
We see that resampling consists of an inner-product between the given samples with a continuous interpolation kernel that is sampled where needed to satisfy the needs of the inner product operation. In the time domain, our interpolation kernel is a scaled sinc function, while in the frequency domain, it is an asinc function. The interpolation kernel can of course be horizontally scaled to alter bandwidth [270], or more generally reshaped to introduce a more general windowing in the opposite domain:
- Width of interpolation kernel (main-lobe width)
 1/width-in-other-domain
1/width-in-other-domain
- Shape of interpolation kernel
 gain profile
(window) in other domain
gain profile
(window) in other domain
Getting back to non-uniform resampling of audio spectra, we have that an auditory-filter frequency-response can be regarded as a frequency-dependent interpolation kernel for nonuniformly resampling the STFT frequency axis. In other words, an auditory filter bank may be implemented as a non-uniform resampling of the uniformly sampled frequency axis provided by an ordinary FFT, using the auditory filter shape as the interpolation kernel.
When the auditory filters vary systematically with frequency, there may be an equivalent non-uniform frequency-warping followed by a uniform sampling of the (warped) frequency axis. Thus, an alternative implementation of an auditory filter bank is to apply an FFT (implementing a uniform filter bank) to a signal having a properly prewarped spectrum, where the warping is designed to approximate whatever auditory frequency axis is desired. This approach is discussed further in Appendix E. (See also §2.5.2.)
Next Section:
Auditory Filter Shapes
Previous Section:
Excitation Pattern



















