DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Polyphase View of the STFT

As a familiar special case, set

$\displaystyle \bold{E}(z) \eqsp \bold{W}_N^\ast$ (12.66)

where $ \bold{W}_N^\ast$ is the DFT matrix:

$\displaystyle \bold{W}_N^\ast[kn] \eqsp \left[e^{-j2\pi kn/N}\right]$ (12.67)

The inverse of this polyphase matrix is then simply the inverse DFT matrix:

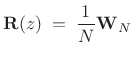$\displaystyle \bold{R}(z) \eqsp \frac{1}{N}\bold{W}_N$ (12.68)

Thus, the STFT (with rectangular window) is the simple special case of a perfect reconstruction filter bank for which the polyphase matrix is constant. It is also unitary; therefore, the STFT is an orthogonal filter bank.

The channel analysis and synthesis filters are, respectively,

\begin{eqnarray*} H_k(z) &=& H_0(zW_N^k)\\ [5pt] F_k(z) &=& F_0(zW_N^{-k}) \end{eqnarray*}

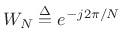where $ W_N\isdef e^{-j2\pi/N}$ , and

$\displaystyle F_0(z)\eqsp H_0(z)\eqsp \sum_{n=0}^{N-1}z^{-n}\;\longleftrightarrow\;[1,1,\ldots,1]$ (12.69)

corresponding to the rectangular window.

Figure 11.25: Polyphase representation of the STFT with a rectangular window.
\includegraphics[width=\twidth]{eps/polyNchanSTFT}

Looking again at the polyphase representation of the $ N$ -channel filter bank with hop size $ R$ , $ \bold{E}(z)=\bold{W}_N^\ast$ , $ \bold{R}(z)=\bold{W}_N$ , $ R$ dividing $ N$ , we have the system shown in Fig.11.25. Following the same analysis as in §11.4.1 leads to the following conclusion:

$\displaystyle \zbox {\hbox{The polyphase representation is an \emph{overlap-add} representation.}} $

Our analysis showed that the STFT using a rectangular window is a perfect reconstruction filter bank for all integer hop sizes in the set $ R\in\{N,N/2,N/3,\ldots,N/N\}$ . The same type of analysis can be applied to the STFT using the other windows we've studied, including Portnoff windows.

Next Section:
Example: Polyphase Analysis of the STFT with 50% Overlap, Zero-Padding, and a Non-Rectangular Window
Previous Section:
Necessary and Sufficient Conditions for Perfect Reconstruction