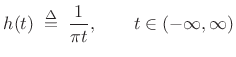DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Primer on Hilbert Transform Theory

We need a Hilbert-transform filter $ {\cal H}$ to compute the imaginary part $ y(t)$ of the analytic signal $ x_a(t)$ given its real part $ x(t)$ . That is,

$\displaystyle x_a(t) \eqsp x(t) + j\,y(t)$ (5.14)

where $ y = {\cal H}\{x\}$ . In the frequency domain, we have

$\displaystyle X_a(\omega) \eqsp X(\omega) + j\,Y(\omega) \eqsp \left[1+j\,H(\omega)\right]\,X(\omega)$ (5.15)

where $ H(\omega)$ denotes the frequency response of the Hilbert transform $ {\cal H}$ . Since by definition we have $ X_a(\omega)=0$ for $ \omega<0$ , we must have $ j\,H(\omega)=-1$ for $ \omega<0$ , so that $ H(\omega)=j$ for negative frequencies (an allpass response with phase-shift $ +90$ degrees). To pass the positive-frequency components unchanged, we would most naturally define $ H(\omega)=0$ for $ \omega>0$ . However, conventionally, the positive-frequency Hilbert-transform frequency response is defined more symmetrically as $ H(\omega)=-j$ for $ \omega>0$ , which gives $ j\,H(\omega)=+1$ and $\mbox{re\ensuremath{\left\{X_a(\omega)\right\}}}=2X(\omega)$ , i.e., the positive-frequency components of $ X$ are multiplied by $ 2$ .

In view of the foregoing, the frequency response of the ideal Hilbert-transform filter may be defined as follows:

$\displaystyle H(\omega) \isdefs \left\{\begin{array}{ll} \quad\! j, & \omega<0 \\ [5pt] \quad\!0, & \omega=0 \\ [5pt] -j, & \omega>0 \\ \end{array} \right. \protect$ (5.16)

Note that the point at $ \omega = 0$ can be defined arbitrarily since the inverse-Fourier transform integral is not affected by a single finite point (being a ``set of measure zero'').

The ideal filter impulse response $ h(n)$ is obtained by finding the inverse Fourier transform of (4.16). For discrete time, we may take the inverse DTFT of (4.16) to obtain the ideal discrete-time Hilbert-transform impulse response, as pursued in Problem 10. We will work with the usual continuous-time limit $ h(t)=1/(\pi t)$ in the next section.

Hilbert Transform

The Hilbert transform $ y(t)$ of a real, continuous-time signal $ x(t)$ may be expressed as the convolution of $ x$ with the Hilbert transform kernel:

$\displaystyle h(t) \isdefs \frac{1}{\pi t},\qquad t\in(-\infty,\infty) \protect$ (5.17)

That is, the Hilbert transform of $ x$ is given by

$\displaystyle y = h \ast x. % \qquad \hbox{(Hilbert transform of $x$)}. $ (5.18)

Thus, the Hilbert transform is a non-causal linear time-invariant filter.

The complex analytic signal $ x_a(t)$ corresponding to the real signal $ x(t)$ is then given by

$\displaystyle x_a(t)$ $\displaystyle \isdef$ $\displaystyle x(t) + j y(t)$  
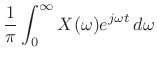$\displaystyle %\qquad \hbox{(Analytic signal corresponding to $x$)}\\ [10pt] $ $\displaystyle =$ $\displaystyle \frac{1}{\pi}\displaystyle\int_0^{\infty} X(\omega)e^{j\omega t}\, d\omega$ (5.19)

To show this last equality (note the lower limit of 0 instead of the usual $ -\infty$ ), it is easiest to apply (4.16) in the frequency domain:

$\displaystyle X_a(\omega)$ $\displaystyle \isdef$ $\displaystyle X(\omega) + j Y(\omega)$  
  $\displaystyle \isdef$ $\displaystyle (X_++X_-) + j (-j X_+ + j X_-)$ (5.20)
  $\displaystyle =$ $\displaystyle 2X_+(\omega)$ (5.21)

Thus, the negative-frequency components of $ X$ are canceled, while the positive-frequency components are doubled. This occurs because, as discussed above, the Hilbert transform is an allpass filter that provides a $ 90$ degree phase shift at all negative frequencies, and a $ -90$ degree phase shift at all positive frequencies, as indicated in (4.16). The use of the Hilbert transform to create an analytic signal from a real signal is one of its main applications. However, as the preceding sections make clear, a Hilbert transform in practice is far from ideal because it must be made finite-duration in some way.

Next Section:
Filtering and Windowing the Ideal Hilbert-Transform Impulse Response
Previous Section:
Bandpass Filter Design Example