Filtering and Windowing the Ideal
Hilbert-Transform Impulse Response
Let ![]() denote the convolution kernel of the continuous-time
Hilbert transform from (4.17) above:
denote the convolution kernel of the continuous-time
Hilbert transform from (4.17) above:
Convolving a real signal
Note that we cannot allow a time-domain sample at time 0 in (4.22) because it would be infinity. Instead, time 0 should be taken to lie between two samples, thereby introducing a small non-integer advance or delay. We'll choose a half-sample delay. As a result, we'll need to delay the real-part filter by half a sample as well when we make a complete single-sideband filter.
The matlab below illustrates the design of an FIR Hilbert-transform
filter by the window method using a Kaiser window. For a more
practical illustration, the sampling-rate assumed is set to
![]() Hz instead of being normalized to 1 as usual. The
Kaiser-window
Hz instead of being normalized to 1 as usual. The
Kaiser-window ![]() parameter is set to
parameter is set to ![]() , which normally gives
``pretty good'' audio performance (cf. Fig.3.28). From
Fig.3.28, we see that we can expect a stop-band attenuation
better than
, which normally gives
``pretty good'' audio performance (cf. Fig.3.28). From
Fig.3.28, we see that we can expect a stop-band attenuation
better than ![]() dB. The choice of
dB. The choice of ![]() , in setting the
time-bandwidth product of the Kaiser window, determines both the
stop-band rejection and the transition bandwidths required by our FIR
frequency response.
, in setting the
time-bandwidth product of the Kaiser window, determines both the
stop-band rejection and the transition bandwidths required by our FIR
frequency response.
M = 257; % window length = FIR filter length (Window Method) fs = 22050; % sampling rate assumed (Hz) f1 = 530; % lower pass-band limit = transition bandwidth (Hz) beta = 8; % beta for Kaiser window for decent side-lobe rejectionRecall that, for a rectangular window, our minimum transition bandwidth would be
Matlab, Continued
Given the above design parameters, we compute some derived parameters as follows:
fn = fs/2; % Nyquist limit (Hz) f2 = fn - f1; % upper pass-band limit N = 2^(nextpow2(8*M)); % large FFT for interpolated display k1 = round(N*f1/fs); % lower band edge in bins if k1<2, k1=2; end; % cannot have dc or fn response kn = N/2 + 1; % bin index at Nyquist limit (1-based) k2 = kn-k1+1; % high-frequency band edge f1 = k1*fs/N % quantized band-edge frequencies f2 = k2*fs/NSetting the upper transition band the same as the low-frequency band (
Kaiser Window
With the filter length ![]() and Kaiser window
and Kaiser window ![]() as given
above, we may compute the Kaiser window itself in matlab via
as given
above, we may compute the Kaiser window itself in matlab via
w = kaiser(M,beta)'; % Kaiser window in "linear phase form"The spectrum of this window (zero-padded by more than a factor of 8) is shown in Fig.4.9 (full magnitude spectrum) and Fig.4.10 (zoom-in on the main lobe).
Windowing a Desired Impulse Response Computed by the
Frequency Sampling Method
The next step is to apply our Kaiser window to the ``desired'' impulse
response, where ``desired'' means a time-shifted (by 1/2 sample) and
bandlimited (to introduce transition bands) version of the ``ideal''
impulse response in (4.22). In principle, we are using the
frequency-sampling method (§4.4) to prepare a
desired FIR filter of length ![]() as the inverse FFT of a desired
frequency response prepared by direct Fourier intuition. This long
FIR filter is then ``windowed'' down to length
as the inverse FFT of a desired
frequency response prepared by direct Fourier intuition. This long
FIR filter is then ``windowed'' down to length ![]() to give us our
final FIR filter designed by the window method.
to give us our
final FIR filter designed by the window method.
If the smallest transition bandwidth is ![]() Hz, then the FFT size
Hz, then the FFT size ![]() should satisfy
should satisfy
![]() . Otherwise, there may be too much time
aliasing in the desired impulse response.5.10 The only non-obvious
part in the matlab below is ``
. Otherwise, there may be too much time
aliasing in the desired impulse response.5.10 The only non-obvious
part in the matlab below is ``.^8'' which smooths the taper to
zero and looks better on a log magnitude scale. It would also make
sense to do a linear taper on a dB scale which corresponds to
an exponential taper to zero.
H = [ ([0:k1-2]/(k1-1)).^8,ones(1,k2-k1+1),...
([k1-2:-1:0]/(k1-1)).^8, zeros(1,N/2-1)];
Figure 4.11 shows our desired amplitude response so constructed.
Now we inverse-FFT the desired frequency response to obtain the desired impulse response:
h = ifft(H); % desired impulse response hodd = imag(h(1:2:N)); % This should be zero ierr = norm(hodd)/norm(h); % Look at numerical round-off error % Typical value: ierr = 4.1958e-15 % Also look at time aliasing: aerr = norm(h(N/2-N/32:N/2+N/32))/norm(h); % Typical value: 4.8300e-04The real part of the desired impulse response is shown in Fig.4.12, and the imaginary part in Fig.4.13.
Now use the Kaiser window to time-limit the desired impulse response:
% put window in zero-phase form: wzp = [w((M+1)/2:M), zeros(1,N-M), w(1:(M-1)/2)]; hw = wzp .* h; % single-sideband FIR filter, zero-centered Hw = fft(hw); % for results display: plot(db(Hw)); hh = [hw(N-(M-1)/2+1:N),hw(1:(M+1)/2)]; % caual FIR % plot(db(fft([hh,zeros(1,N-M)]))); % freq resp plot
Figure 4.14 and Fig.4.15
show the normalized dB magnitude frequency response of our
final FIR filter consisting of the ![]() nonzero samples of
hw.
nonzero samples of
hw.
Next Section:
More General FIR Filter Design
Previous Section:
Primer on Hilbert Transform Theory








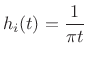
![\includegraphics[width=0.8\twidth]{eps/KaiserFR}](http://www.dsprelated.com/josimages_new/sasp2/img792.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserZoomFR}](http://www.dsprelated.com/josimages_new/sasp2/img793.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertFRIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img796.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertIRRealIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img797.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertIRImagIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img798.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserHilbertFR}](http://www.dsprelated.com/josimages_new/sasp2/img799.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserHilbertZoomedFR}](http://www.dsprelated.com/josimages_new/sasp2/img800.png)











