DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sample-Variance Variance

Consider now the sample variance estimator

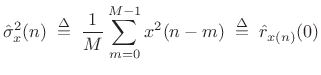$\displaystyle \hat{\sigma}_x^2(n) \isdefs \frac{1}{M}\sum_{m=0}^{M-1}x^2(n-m) \isdefs \hat{r}_{x(n)}(0)$ (C.33)

where the mean is assumed to be $ \mu_x ={\cal E}\left\{x(n)\right\}=0$ , and $ \hat{r}_{x(n)}(l)$ denotes the unbiased sample autocorrelation of $ x$ based on the $ M$ samples leading up to and including time $ n$ . Since $ \hat{r}_{x(n)}(0)$ is unbiased, $ {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} = {\cal E}\left\{\hat{r}_{x(n)}^2(0)\right\} = \sigma_x^2$ . The variance of this estimator is then given by

\begin{eqnarray*} \mbox{Var}\left\{\hat{\sigma}_x^2(n)\right\} &\isdef & {\cal E}\left\{[\hat{\sigma}_x^2(n)-\sigma_x^2]^2\right\}\\ &=& {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2-\sigma_x^4\right\} \end{eqnarray*}

where

\begin{eqnarray*} {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}{\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\}\\ &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}r_{x^2}(\vert m_1-m_2\vert) \end{eqnarray*}

The autocorrelation of $ x^2(n)$ need not be simply related to that of $ x(n)$ . However, when $ x$ is assumed to be Gaussian white noise, simple relations do exist. For example, when $ m_1\ne m_2$ ,

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = {\cal E}\left\{x^2(n-m_1)\right\}{\cal E}\left\{x^2(n-m_2)\right\}=\sigma_x^2\sigma_x^2= \sigma_x^4.$ (C.34)

by the independence of $ x(n-m_1)$ and $ x(n-m_2)$ , and when $ m_1=m_2$ , the fourth moment is given by $ {\cal E}\left\{x^4(n)\right\} = 3\sigma_x^4$ . More generally, we can simply label the $ k$ th moment of $ x(n)$ as $ \mu_k = {\cal E}\left\{x^k(n)\right\}$ , where $ k=1$ corresponds to the mean, $ k=2$ corresponds to the variance (when the mean is zero), etc.

When $ x(n)$ is assumed to be Gaussian white noise, we have

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = \left\{\begin{array}{ll} \sigma_x^4, & m_1\ne m_2 \\ [5pt] 3\sigma_x^4, & m_1=m_2 \\ \end{array} \right.$ (C.35)

so that the variance of our estimator for the variance of Gaussian white noise is

Var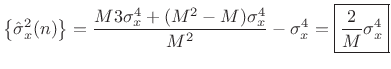$\displaystyle \left\{\hat{\sigma}_x^2(n)\right\} = \frac{M3\sigma_x^4 + (M^2-M)\sigma_x^4}{M^2} - \sigma_x^4 = \zbox {\frac{2}{M}\sigma_x^4}$ (C.36)

Again we see that the variance of the estimator declines as $ 1/M$ .

The same basic analysis as above can be used to estimate the variance of the sample autocorrelation estimates for each lag, and/or the variance of the power spectral density estimate at each frequency.

As mentioned above, to obtain a grounding in statistical signal processing, see references such as [201,121,95].

Next Section:
Uniform Distribution
Previous Section:
Sample-Mean Variance