DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Shift Theorem for the DTFT

We define the shift operator for sampled signals $ x(n)$ by

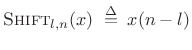$\displaystyle \hbox{\sc Shift}_{l,n}(x) \isdefs x(n-l)$ (3.18)

where $ l$ is any integer ( $ l\in{\bf Z}$ ). Thus, $ \hbox{\sc Shift}_l(x)$ is a right-shift or delay by $ l$ samples.

The shift theorem states3.5

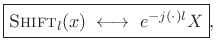$\displaystyle \zbox {\hbox{\sc Shift}_l(x) \;\longleftrightarrow\;e^{-j(\cdot)l}X},$ (3.19)

or, in operator notation,

$\displaystyle \hbox{\sc DTFT}_\omega[\hbox{\sc Shift}_l(x)] \eqsp \left( e^{-j\omega l} \right) X(\omega)$ (3.20)


Proof:

\begin{eqnarray*} \hbox{\sc DTFT}_\omega[\hbox{\sc Shift}_l(x)] &\isdef & \sum_{n=-\infty}^{\infty}x(n-l) e^{-j \omega n} \\ &=& \sum_{m=-\infty}^{\infty} x(m) e^{-j \omega (m+l)} \qquad(m\isdef n-l) \\ &=& \sum_{m=-\infty}^{\infty}x(m) e^{-j \omega m} e^{-j \omega l} \\ &=& e^{-j \omega l} \sum_{m=-\infty}^{\infty}x(m) e^{-j \omega m} \\ &\isdef & e^{-j \omega l} X(\omega) \end{eqnarray*}

Note that $ e^{-j\omega l}$ is a linear phase term, so called because it is a linear function of frequency with slope equal to $ -l$ :

$\displaystyle \angle \left(e^{-j \omega l}\right) \eqsp -\omega l$ (3.21)

The shift theorem gives us that multiplying a spectrum $ X(\omega)$ by a linear phase term $ e^{-j\omega l}$ corresponds to a delay in the time domain by $ l$ samples. If $ l<0$ , it is called a time advance by $ \vert l\vert$ samples.

Next Section:
Convolution Theorem for the DTFT
Previous Section:
Symmetry of the DTFT for Real Signals