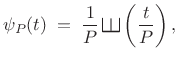DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Impulse Trains

The impulse signal $ \delta(t)$ (defined in §B.10) has a constant Fourier transform:

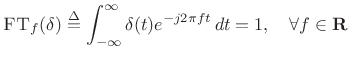$\displaystyle \hbox{\sc FT}_f(\delta) \isdef \int_{-\infty}^\infty \delta(t) e^{-j2\pi f t}\,dt = 1, \quad \forall f\in{\bf R}$ (B.43)

An impulse train can be defined as a sum of shifted impulses:

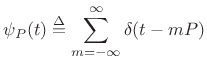$\displaystyle \psi_P(t) \isdef \sum_{m=-\infty}^\infty \delta(t-mP)$ (B.44)

Here, $ P$ is the period of the impulse train, in seconds--i.e., the spacing between successive impulses. The $ P$ -periodic impulse train can also be defined as

$\displaystyle \psi_P(t)\eqsp \frac{1}{P}\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}\left(\frac{t}{P}\right), \protect$ (B.45)

where $ \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(t)$ is the so-called shah symbol [23]:

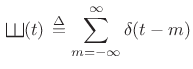$\displaystyle {\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(t) \, \isdef \sum_{m=-\infty}^\infty \delta(t-m)}$ (B.46)

Note that the scaling by $ 1/P$ in (B.46) is necessary to maintain unit area under each impulse.

We will now show that

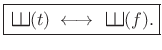$\displaystyle \zbox {\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(t)\;\longleftrightarrow\;\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(f).}$ (B.47)

That is, the Fourier transform of the normalized impulse train $ \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(t)$ is exactly the same impulse train $ \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(f)$ in the frequency domain, where $ t$ denotes time in seconds and $ f$ denotes frequency in Hz. By the scaling theorem (§B.4),

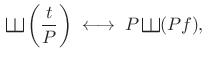$\displaystyle {\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}\left(\frac{t}{P}\right) \;\longleftrightarrow\;P\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(Pf),}$ (B.48)

so that the $ P$ -periodic impulse-train defined in (B.46) transforms to

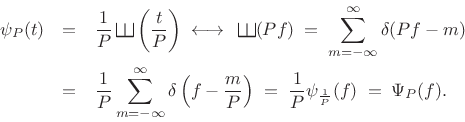
\begin{eqnarray*} \psi_P(t) &=& \frac{1}{P}\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}\left(\frac{t}{P}\right) \;\longleftrightarrow\;\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(Pf) \eqsp \sum_{m=-\infty}^\infty \delta(Pf-m)\\ &=& \frac{1}{P}\sum_{m=-\infty}^\infty \delta\left(f-\frac{m}{P}\right) \eqsp \frac{1}{P}\psi_{\frac{1}{P}}(f) \eqsp \Psi_P(f). \end{eqnarray*}

Thus, the $ P$ -periodic impulse train transforms to a $ (1/P)$ -periodic impulse train, in which each impulse contains area $ 1/P$ :

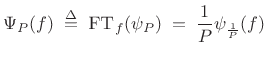$\displaystyle {\Psi_P(f) \isdefs \hbox{\sc FT}_f(\psi_P) \eqsp \frac{1}{P}\psi_{\frac{1}{P}}(f)}$ (B.49)


Proof: Let's set up a limiting construction by defining

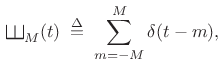$\displaystyle \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M(t) \isdefs \sum_{m=-M}^M \delta(t-m),$ (B.50)

so that $ \lim_{M\to\infty}\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M(t)=\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(t)$ . We may interpret $ \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M(t)$ as a sampled rectangular pulse of width $ 2M$ seconds (yielding $ 2M+1$ samples).By linearity of the Fourier transform and the shift theorem (§B.5), we readily obtain the transform of $ \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M(t)$ to be

\begin{eqnarray*} \hbox{\sc FT}_f(\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M) &\isdef & \hbox{\sc FT}_f\left[\sum_{m=-M}^M \hbox{\sc Shift}_{m}(\delta)\right]\\ &=& \sum_{m=-M}^M \hbox{\sc FT}_f[\hbox{\sc Shift}_{m}(\delta)] \eqsp \sum_{m=-M}^M e^{-j2\pi f m}. \end{eqnarray*}

Using the closed form of a geometric series,

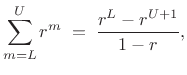$\displaystyle \sum_{m=L}^U r^m \eqsp \frac{ r^L - r^{U+1}}{1-r},$ (B.51)

with $ r=e^{-j\pi f}$ , we can write this as

\begin{eqnarray*} \hbox{\sc FT}_f(\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M) &=& \frac{e^{j2\pi f M } - e^{-j2\pi f M } e^{-j2\pi f }}{1-e^{-j2\pi f }}\\ [10pt] &=& \frac{e^{-j\pi f}}{e^{-j\pi f}} \cdot \frac{e^{j\pi f (2M+1) } - e^{-j\pi f (2M+1) }}{e^{j\pi f}-e^{-j\pi f}}\\ [10pt] &=& \frac{\sin[\pi f (2M+1) ]}{\sin(\pi f)}\\ [5pt] &\isdef & (2M+1)\,\hbox{asinc}_{2M+1}(2\pi f ) \end{eqnarray*}

where we have used the definition of $ \hbox{asinc}$ given in Eq.$ \,$ (3.5) of §3.1. As we would expect from basic sampling theory, the Fourier transform of the sampled rectangular pulse is an aliased sinc function. Figure 3.2 illustrates one period $ M\cdot\hbox{asinc}_M(\omega)$ for $ M=11$ .

The proof can be completed by expressing the aliased sinc function as a sum of regular sinc functions, and using linearity of the Fourier transform to distribute $ \hbox{\sc FT}_f$ over the sum, converting each sinc function into an impulse, in the limit, by §B.13:

\begin{eqnarray*} (2M+1)\,\hbox{asinc}_{2M+1}(2\pi f) &\isdef & \frac{\sin[\pi f (2M+1) ]}{\sin(\pi f)}\\ [5pt] &=& \sum_{k=-\infty}^{\infty} \mbox{sinc}(2Mf-k)\\ [5pt] &\to& \sum_{k=-\infty}^{\infty} \delta(f-k) \end{eqnarray*}

by §B.13. Note that near $ f=0,2,4,\ldots$ , we have

\begin{eqnarray*} \hbox{\sc FT}_f(\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M) &=& \frac{\sin[\pi f (2M+1) ]}{\sin(\pi f)} \;\;\approx\;\; \frac{\sin[\pi f (2M+1) ]}{\pi f}\\ [5pt] &=&(2M+1)\mbox{sinc}[(2M+1)f] \;\;\to\;\;\delta(f) \end{eqnarray*}

as $ M\to\infty$ , as shown in §B.13. Similarly, near $ f=1,3,5,\ldots$ , we have

$\displaystyle \hbox{\sc FT}_f(\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}_M) \;\;\approx\;\; \frac{\sin[\pi f (2M+1) ]}{-\pi f} \;\;\to\;\;\delta(f)$ (B.52)

as $ M\to\infty$ . Finally, we expect that the limit for non-integer $ f$ can be neglected since

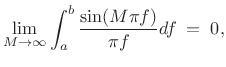$\displaystyle \lim_{M\to\infty}\int_a^b \frac{\sin(M\pi f)}{\pi f} df \eqsp 0,$ (B.53)

whenever $ n<a\leq b<n+1$ and $ n$ is some integer, as implied by §B.13.

See, e.g., [23,79] for more about impulses and their application in Fourier analysis and linear systems theory.

Exercise: Using a similar limiting construction as before,

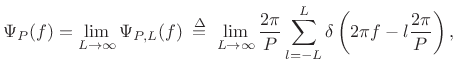$\displaystyle \Psi_P(f) = \lim_{L\to\infty} \Psi_{P,L}(f) \isdefs \lim_{L\to\infty} \frac{2\pi}{P}\sum_{l=-L}^L \delta\left(2\pi f-l\frac{2\pi}{P}\right),$ (B.54)

show that a direct inverse-Fourier transform calculation gives

$\displaystyle \psi_{P,L}(t) = \frac{\sin\left[\pi(2L+1)\frac{t}{P}\right]}{\sin\left( \pi \frac{t}{P}\right)},$ (B.55)

and verify that the peaks occur every $ P$ seconds and reach height $ (2L+1)/P$ . Also show that the peak widths, measured between zero crossings, are $ P/(2L+1)$ , so that the area under each peak is of order 1 in the limit as $ L\to\infty$ . [Hint: The shift theorem for inverse Fourier transforms is $ e^{j\nu t}x(t) \;\leftrightarrow\; X(f-\nu)$ , and $ \hbox{\sc IFT}_t(\delta)=1/(2\pi)$ .]

Next Section:
Poisson Summation Formula
Previous Section:
Sinc Impulse