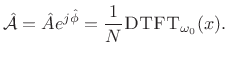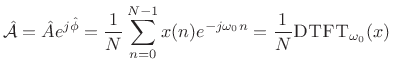DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sinusoidal Amplitude and Phase Estimation

The form of the optimal estimator (5.39) immediately suggests the following generalization for the case of unknown amplitude and phase:

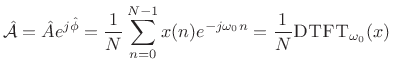$\displaystyle \hat{{\cal A}}= {\hat A}e^{j\hat{\phi}} = \frac{1}{N}\sum_{n=0}^{N-1} x(n) e^{-j\omega_0 n} = \frac{1}{N}\hbox{\sc DTFT}_{\omega_0 }(x) \protect$ (6.41)

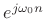
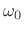
That is, $ \hat{{\cal A}}$ is given by the complex coefficient of projection [264] of $ x$ onto the complex sinusoid $ e^{j\omega_0 n}$ at the known frequency $ \omega_0$ . This can be shown by generalizing the previous derivation, but here we will derive it using the more enlightened orthogonality principle [114].

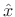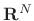The orthogonality principle for linear least squares estimation states that the projection error must be orthogonal to the model. That is, if $ {\hat x}$ is our optimal signal model (viewed now as an $ N$ -vector in $ {\bf R}^N$ ), then we must have [264]

\begin{eqnarray*} x-{\hat x}&\perp& {\hat x}\\ \Rightarrow\quad \left<x-{\hat x},{\hat x}\right> &=& 0\\ \Rightarrow\quad \left<x,{\hat x}\right> &=& \left<{\hat x},{\hat x}\right>\\ \Rightarrow\quad \sum_{n=0}^{N-1}\overline{x(n)} {\hat A}e^{j(\omega_0 n+\hat{\phi})}&=& N {\hat A}^2 \\ \Rightarrow\quad \sum_{n=0}^{N-1}x(n) {\hat A}e^{-j(\omega_0 n+\hat{\phi})}&=& N {\hat A}^2 \\ \Rightarrow\quad \hbox{\sc DTFT}_{\omega_0 }(x)&=& N \frac{{\hat A}^2}{{\hat A}e^{-j\hat{\phi}}} = N {\hat A}e^{j\hat{\phi}} \end{eqnarray*}

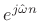Thus, the complex coefficient of projection of $ x$ onto $ e^{j{\hat \omega}n}$ is given by

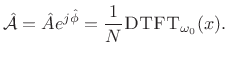$\displaystyle \hat{{\cal A}}= {\hat A}e^{j\hat{\phi}} = \frac{1}{N} \hbox{\sc DTFT}_{\omega_0 }(x).$ (6.42)

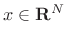
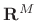
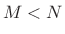
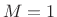
The optimality of $ \hat{{\cal A}}$ in the least squares sense follows from the least-squares optimality of orthogonal projection [114,121,252]. From a geometrical point of view, referring to Fig.5.16, we say that the minimum distance from a vector $ x\in{\bf R}^N$ to some lower-dimensional subspace $ {\bf R}^M$ , where $ M<N$ (here $ M=1$ for one complex sinusoid) may be found by ``dropping a perpendicular'' from $ x$ to the subspace. 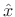The point $ {\hat x}$ at the foot of the perpendicular is the point within the subspace closest to $ x$ in Euclidean distance.

Figure: Geometric interpretation of the orthogonal projection of a vector $ x$ in 3D space onto a 2D plane ($ N=3$ , $ M=2$ ). The orthogonal projection $ {\hat x}$ minimizes the Euclidean distance $ \left\Vert\,x-{\hat x}\,\right\Vert$ .
\includegraphics{eps/orthproj}

Next Section:
Sinusoidal Frequency Estimation
Previous Section:
Sinusoidal Amplitude Estimation