DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sinusoidal Peak Finding

For each sinusoidal component of a signal, we need to determine its frequency, amplitude, and phase (when needed). As a starting point, consider the windowed complex sinusoid with complex amplitude $ {\cal A}_x$ and frequency $ \omega _x$ :

$\displaystyle x_w(n) = w(n){\cal A}_xe^{j\omega_x nT}$ (11.20)

As discussed in Chapter 5, the transform (DTFT) of this windowed signal is the convolution of a frequency domain delta function at $ \omega _x$ [ $ \delta(\omega - \omega_x) $ ], and the transform of the window function, $ W(\omega)$ , resulting in a shifted version of the window transform $ {\cal A}_xW(\omega-\omega_x)$ . Assuming $ M$ is odd, we can show this as follows:

\begin{eqnarray*} X_w(\omega) &=& \sum_{n=-\infty}^{\infty}[w(n)x(n)]e^{ -j\omega nT} \qquad\hbox{(DTFT($x_w$))} \\ &=& \sum_{n=-(M-1)/2}^{(M-1)/2} \left[w(n){\cal A}_xe^{j\omega_xnT}\right]e^{ -j\omega nT}\\ &=& {\cal A}_x\sum_n w(n) e^{-j(\omega-\omega_x)nT} \\ &=& \zbox {{\cal A}_xW(\omega-\omega_x)} \end{eqnarray*}

Hence,

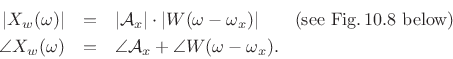
\begin{eqnarray*} \vert X_w(\omega) \vert &=& \vert{\cal A}_x\vert \cdot \vert W(\omega-\omega_x)\vert \qquad \hbox{(see \fref {peak} below)}\\ \angle X_w(\omega) &=& \angle {\cal A}_x+ \angle W(\omega-\omega_x). \end{eqnarray*}

At $ \omega _x$ , we have

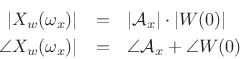
\begin{eqnarray*} \vert X_w(\omega_x)\vert &=& \vert{\cal A}_x\vert\cdot \vert W(0)\vert \\ \angle X_w(\omega_x)\vert &=& \angle {\cal A}_x+ \angle W(0) \end{eqnarray*}

If we scale the window to have a dc gain of 1, then the peak magnitude equals the amplitude of the sinusoid, i.e., 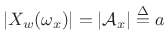$ \vert X_w(\omega_x)\vert=\vert{\cal A}_x\vert\isdef a$ , as shown in Fig.10.8.

Figure: Schematic diagram of a window transform amplitude-scaled by $ a$ and frequency-shifted by $ \omega _x$ .
\includegraphics[width=0.8\twidth]{eps/peak}

If we use a zero-phase (even) window, the phase at the peak equals the phase of the sinusoid, i.e., $ \angle X_w(\omega_x) = \angle {\cal A}_x$ .

Next Section:
Tracking Sinusoidal Peaks in a Sequence of FFTs
Previous Section:
Following Spectral Peaks