DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Spectrum of Sampled Complex Sinusoid

In the discrete-time case, we replace $ t$ by $ nT$ where $ n$ ranges over the integers and $ T$ is the sampling period in seconds. Thus, for the positive-frequency component of the sinusoid of the previous section, we obtain

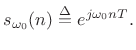$\displaystyle s_{\omega_0}(n) \isdef e^{j\omega_0 n T}.$ (6.8)

It is common notational practice in signal processing to use normalized radian frequency

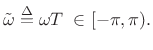$\displaystyle {\tilde \omega}\isdef \omega T \;\in[-\pi,\pi).$ (6.9)

Thus, our sampled complex sinusoid becomes

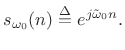$\displaystyle s_{\omega_0}(n) \isdef e^{j{\tilde \omega}_0 n}.$ (6.10)

It is not difficult to convert between normalized and unnormalized frequency. The use of a tilde (` $ \tilde{\null}$ ') will explicitly indicate normalization, but it may be left off as well, so that $ \omega$ may denote either normalized or unnormalized frequency.6.4

The spectrum of infinitely long discrete-time signals is given by the Discrete Time Fourier Transform (DTFT) (discussed in §2.1):

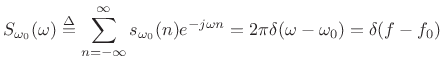$\displaystyle S_{\omega_0}(\omega) \isdef \sum_{n=-\infty}^{\infty} s_{\omega_0}(n) e^{-j\omega n} = 2\pi\delta(\omega-\omega_0) = \delta(f-f_0)$ (6.11)

where now $ \delta(\omega)$ is an impulse defined for $ \omega\in[-\pi,\pi)$ or $ f\in\left[-\frac{1}{2},\frac{1}{2}\right)$ , and $ \omega$ denotes normalized radian frequency. (Treatments of the DTFT invariably use normalized frequency.)

Next Section:
Spectrum of a Windowed Sinusoid
Previous Section:
Spectrum of a Sinusoid