Spectrum of a Windowed Sinusoid
Ideal sinusoids are infinite in duration. In practice, however, we must work with finite-length signals. Therefore, only a finite segment of a sinusoid can be processed at any one time, as if we were looking at the sinusoid through a ``window'' in time. For audio signals, the ear also processes sinusoids in short time windows (much less than 1 second long); thus, audio spectrum analysis is generally carried out using analysis windows comparable to the time-window inherent in hearing. Finally, nothing in nature produces true sinusoids. However, natural oscillations can often be modeled as sinusoidal over some finite time. Thus, it is useful to consider short-time spectrum analysis, in which the time-domain signal is analyzed in short time segments (windows). The short-time spectrum then evolves at some rate over time. The shorter our analysis window, the faster the short-time spectrum can change. Very long analysis windows, on the other hand, presuppose a fixed spectral content over the duration of the window.
The easiest windowing operation is simply truncating the sinusoid on the left and right at some finite times. This can be modeled mathematically as a multiplication of the sinusoid by the so-called rectangular window:
![$\displaystyle w_R(n) \isdef \left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img349.png) |
(6.12) |
where
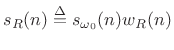 |
(6.13) |
However, as we will see, it is often advantageous to taper the window more gracefully to zero on the left and right. Figure 5.1 illustrates the general shape of a more typical window function. Note that it is nonnegative and symmetric about time 0. Such functions are loosely called ``zero-phase'' since their Fourier transforms are real, as shown in §2.3. A more precise adjective is zero-centered for such windows.
In some cases, such as when analyzing real time systems, it is
appropriate to require our analysis windows be causal.
A window ![]() is said to be causal if it is zero for all
is said to be causal if it is zero for all ![]() .
Figure 5.2 depicts the causal version of the window shown in
Fig.5.1. A length
.
Figure 5.2 depicts the causal version of the window shown in
Fig.5.1. A length ![]() zero-centered
window can be made causal by shifting
(delaying) it in time by half its length
zero-centered
window can be made causal by shifting
(delaying) it in time by half its length ![]() . The shift theorem
(§2.3.4) tells us this introduces a linear phase term in
the frequency domain. That is, the window Fourier transform has gone
from being real to being multiplied by
. The shift theorem
(§2.3.4) tells us this introduces a linear phase term in
the frequency domain. That is, the window Fourier transform has gone
from being real to being multiplied by
![]() .
.
Next Section:
Effect of Windowing
Previous Section:
Spectrum of Sampled Complex Sinusoid








![\includegraphics[width=4in]{eps/generalWindow}](http://www.dsprelated.com/josimages_new/sasp2/img925.png)
![\includegraphics[width=3.5in]{eps/causalWindow}](http://www.dsprelated.com/josimages_new/sasp2/img927.png)











