Free Books
   Free Books    Spectral Audio Signal Processing  

Spectrum of a Sinusoid

A sinusoid is any signal of the form

$\displaystyle x(t) = A\cos(\omega_0 t + \phi), \quad t\in{\bf R}$ (6.1)

where $ A$ is the amplitude (in arbitrary units), $ \phi\in[-\pi,\pi)$ is the phase in radians, and $ \omega_0$ is the frequency in radians per second. Time $ t$ is a real number that varies continuously from minus infinity to infinity in the ideal sinusoid. All three parameters $ (A,\omega_0,\phi)$ are real numbers. In addition to radian frequency $ \omega$ , it is useful to define $ \omega = 2\pi f$ , where $ f$ is the frequency in Hertz (Hz).6.1

By Euler's identity, $ e^{j\theta} = \cos(\theta) + j\sin(\theta)$ , we can write

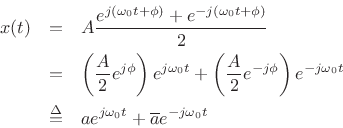
\begin{eqnarray*} x(t) &=& A \frac{e^{j(\omega_0 t + \phi)} + e^{-j(\omega_0 t + \phi)}}{2}\\ &=& \left(\frac{A}{2}e^{j \phi}\right) e^{j\omega_0 t} + \left(\frac{A}{2}e^{-j \phi}\right) e^{-j\omega_0 t}\\ &\isdef & a e^{j\omega_0 t} + \overline{a} e^{-j\omega_0 t} \end{eqnarray*}

where $ \overline{a}$ denotes the complex conjugate of $ a$ . Thus, we can build a real sinusoid $ x(t)$ as a linear combination of positive- and negative-frequency complex sinusoidal components:

$\displaystyle x(t) = a s_{\omega_0}(t) + \overline{a} s_{-\omega_0}(t) \protect$ (6.2)

where

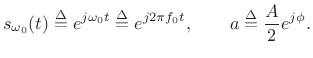$\displaystyle s_{\omega_0}(t) \isdef e^{j\omega_0 t} \isdef e^{j2\pi f_0 t}, \qquad a\isdef \frac{A}{2}e^{j\phi}.$ (6.3)

The spectrum of $ x(t)$ is given by its Fourier transform (see §2.2):

\begin{eqnarray*} X(\omega) &\isdef & \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt\nonumber \\ [5pt] &=& \int_{-\infty}^{\infty} \left[a s_{\omega_0}(t) + \overline{a} s_{-\omega_0}(t) \right] e^{-j\omega t} dt. \end{eqnarray*}

In this case, $ x(t)$ is given by (5.2) and we have

$\displaystyle X(\omega) = a S_{\omega_0}(\omega) + \overline{a} S_{-\omega_0}(\omega). \protect$ (6.4)

We see that, since the Fourier transform is a linear operator, we need only work with the unit-amplitude, zero-phase, positive-frequency sinusoid 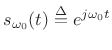$ s_{\omega_0}(t)\isdef e^{j\omega_0t}$ . For $ \omega_0>0$ , $ as_{\omega_0}(t)$ may be called the analytic signal corresponding to $ x(t)$ .6.2

It remains to find the Fourier transform of $ s_{\omega_0}(t)$ :

\begin{eqnarray*} S_{\omega_0}(\omega) &=& \int_{-\infty}^{\infty} s_{\omega_0}(t) e^{-j\omega t} dt\\ [5pt] &\isdef & \int_{-\infty}^{\infty} e^{j\omega_0 t} e^{-j\omega t} dt\\ [5pt] &=& \int_{-\infty}^{\infty} e^{j(\omega_0-\omega) t} dt\\ [5pt] &=& \left.\frac{1}{j(\omega_0-\omega)} e^{j(\omega_0-\omega) t} \right\vert _{-\infty}^\infty\\ [5pt] &=& \lim_{\Delta\to\infty} 2\frac{\sin[(\omega_0-\omega)\Delta]}{\omega_0-\omega}\\ [5pt] &=& 2\pi\delta(\omega_0-\omega) = \delta(f_0-f), \end{eqnarray*}

where $ \delta(\omega)$ is the delta function or impulse at frequency $ \omega_0$ (see Fig.5.4 for a plot, and §B.10 for a mathematical introduction). Since the delta function is even ( $ \delta(-\omega) = \delta(\omega)$ ), we can also write $ S_{\omega_0}(\omega) = 2\pi\delta(\omega-\omega_0) = \delta(f-f_0)$ . It is shown in §B.13 that the sinc limit above approaches a delta function $ \delta(f_0-f)$ . However, we will only use the Discrete Fourier Transform (DFT) in any practical applications, and in that case, the result is easy to show [264].

The inverse Fourier transform is easy to evaluate by the sifting property6.3of delta functions:

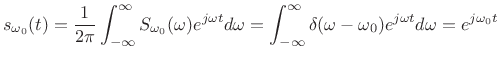$\displaystyle s_{\omega_0}(t) = \frac{1}{2\pi}\int_{-\infty}^\infty S_{\omega_0}(\omega) e^{j\omega t} d\omega = \int_{-\infty}^\infty \delta(\omega-\omega_0) e^{j\omega t} d\omega = e^{j\omega_0 t}$ (6.6)

Substituting into (5.4), the spectrum of our original sinusoid $ x(t)$ is given by

$\displaystyle X(\omega) = 2\pi\left[a \delta(\omega-\omega_0) + \overline{a}\delta(\omega+\omega_0)\right]$ (6.7)

which is a pair of impulses, one at frequency $ \omega=\omega_0$ having complex amplitude $ 2\pi a = A \pi e^{j\phi}$ , summed with another at frequency $ \omega=-\omega_0$ with complex amplitude $ 2\pi\overline{a} = A\pi e^{-j\phi}$ .

Next Section:
Spectrum of Sampled Complex Sinusoid
Previous Section:
Optimal FIR Digital Filter Design