Weighted Overlap Add
In the weighted overlap add (WOLA) method, we apply a second window after the inverse DFT [49] and prior to the final overlap-add to create the output signal. Such a window can be called a ``synthesis window,'' ``postwindow,'' or simply ``output window.''
Output windows are important in audio compression applications for minimizing ``blocking effects.'' The synthesis window ``fades out'' any spectral coding error at the frame boundaries, thereby suppressing audible discontinuities.
Output windows are not used in simple FFT convolution processors because the input frames are supposed to be expanded by the convolution, and a synthesis window would ``pinch off'' the ``filter ringing'' from each block, yielding incorrect results. Output windows can always be used in conjunction with spectral modifications made by means of the ``filter bank summation'' (FBS) method, which is the subject of the next chapter.
The WOLA method is most useful for nonlinear ``instantaneous'' FFT processors such as
- perceptual audio coders,
- time-scale modification, or
- pitch-shifters.
WOLA Processing Steps
The sequence of operations in a WOLA processor can be expressed as follows:
- Extract the
 th windowed frame of data
th windowed frame of data
 ,
,
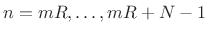 (assuming a length
(assuming a length  causal window
causal window 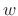 and hop
size
and hop
size  ).
).
- Take an FFT of the
 th frame translated to time zero,
th frame translated to time zero,
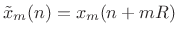 , to produce the
, to produce the  th spectral frame
th spectral frame
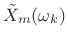 ,
,
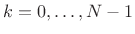 .
.
- Process
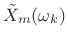 as desired to produce
as desired to produce
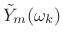 .
.
- Inverse FFT
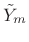 to produce
to produce
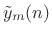 ,
,
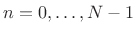 .
.
- Apply a synthesis window
 to
to
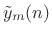 to yield a
weighted output frame
to yield a
weighted output frame
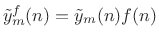 ,
,
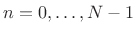 .
.
- Translate the
 th output frame to time
th output frame to time 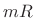 as
as
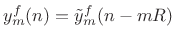 and add to the accumulated output signal
and add to the accumulated output signal 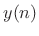 .
.
To obtain perfect reconstruction in the absence of spectral modifications, we require
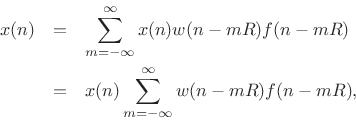
which is true if and only if
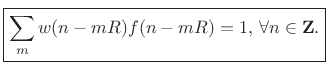 |
(9.44) |
Choice of WOLA Window
The synthesis (output) window in weighted overlap-add is typically chosen to be the same as the analysis (input) window, in which case the COLA constraint becomes
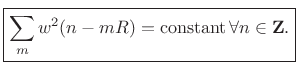 |
(9.45) |
We can say that
A trivial way to construct useful windows for WOLA is to take the
square root of any good OLA window. This works for all non-negative
OLA windows (which covers essentially all windows in Chapter 3
other than Portnoff windows). For example, the
``root-Hann window'' can be defined for odd ![]() by
by
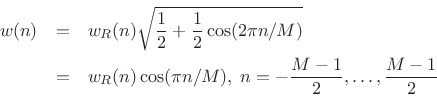
Notice that the root-Hann window is the same thing as the ``MLT Sine Window'' described in §3.2.6. We can similarly define the ``root-Hamming'', ``root-Blackman'', and so on, all of which give perfect reconstruction in the weighted overlap-add context.
Next Section:
Review of Zero Padding
Previous Section:
Time Varying OLA Modifications




















