Spectrum Analysis Windows
In spectrum analysis of naturally occurring audio signals, we
nearly always analyze a short segment of a signal, rather than
the whole signal. This is the case for a variety of reasons.
Perhaps most fundamentally, the ear
similarly Fourier analyzes only a short
segment of audio signals at a time (on the order of 10-20 ms worth).
Therefore, to perform a spectrum analysis having time- and
frequency-resolution comparable to human hearing, we must limit
the time-window accordingly.
We will see that the proper way to extract a ``short time segment'' of
length ![]() from a longer signal is to multiply it by a window
function such as the Hann window:
from a longer signal is to multiply it by a window
function such as the Hann window:
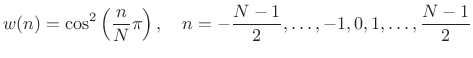 |
(4.1) |
We will see that the main benefit of choosing a good Fourier analysis window function is minimization of side lobes, which cause ``cross-talk'' in the estimated spectrum from one frequency to another.
The study of spectrum-analysis windows serves other purposes as well. Most immediately, it provides an array of useful window types which are best for different situations. Second, by studying windows and their Fourier transforms, we build up our knowledge of Fourier dualities in general. Finally, the defining criteria for different window types often involve interesting and useful analytical techniques.
In this chapter, we begin with a summary of the rectangular window, followed by a variety of additional window types, including the generalized Hamming and Blackman-Harris families (sums of cosines), Bartlett (triangular), Poisson (exponential), Kaiser (Bessel), Dolph-Chebyshev, Gaussian, and other window types.
The Rectangular Window
The (zero-centered) rectangular window may be defined by
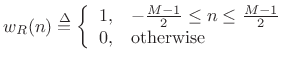 |
(4.2) |
where
To see what happens in the frequency domain, we need to look at the DTFT of the window:
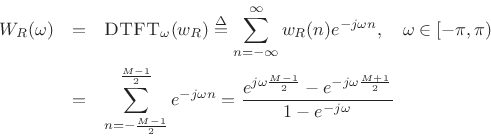
where the last line was derived using the closed form of a geometric series:
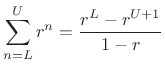 |
(4.3) |
We can factor out linear phase terms from the numerator and denominator of the above expression to get
where
(also called the Dirichlet function [175,72] or periodic sinc function). This (real) result is for the zero-centered rectangular window. For the causal case, a linear phase term appears:
| (4.6) |
The term ``aliased sinc function'' refers to the fact that it may be
simply obtained by sampling the length-![]() continuous-time rectangular window, which has Fourier transform
sinc
continuous-time rectangular window, which has Fourier transform
sinc![]() (given amplitude
(given amplitude
![]() in the time domain). Sampling at intervals of
in the time domain). Sampling at intervals of ![]() seconds in
the time domain corresponds to aliasing in the frequency domain over
the interval
seconds in
the time domain corresponds to aliasing in the frequency domain over
the interval ![]() Hz, and by direct derivation, we have found the
result. It is interesting to consider what happens as the window
duration increases continuously in the time domain: the magnitude
spectrum can only change in discrete jumps as new samples are
included, even though it is continuously parametrized in
Hz, and by direct derivation, we have found the
result. It is interesting to consider what happens as the window
duration increases continuously in the time domain: the magnitude
spectrum can only change in discrete jumps as new samples are
included, even though it is continuously parametrized in ![]() .
.
As the sampling rate goes to infinity, the aliased sinc function therefore approaches the sinc function
Specifically,
where
Figure 3.2 illustrates
![]() for
for ![]() . Note that this is the complete
window transform, not just its real part. We obtain real window
transforms like this only for zero-centered, symmetric windows. Note
that the phase of rectangular-window transform
. Note that this is the complete
window transform, not just its real part. We obtain real window
transforms like this only for zero-centered, symmetric windows. Note
that the phase of rectangular-window transform
![]() is
zero for
is
zero for
![]() , which is the width of the
main lobe. This is why zero-centered windows are often called
zero-phase windows; while the phase
actually alternates between 0
and
, which is the width of the
main lobe. This is why zero-centered windows are often called
zero-phase windows; while the phase
actually alternates between 0
and ![]() radians, the
radians, the ![]() values
occur only within side-lobes which are routinely neglected (in fact,
the window is normally designed to ensure that all side-lobes can be
neglected).
values
occur only within side-lobes which are routinely neglected (in fact,
the window is normally designed to ensure that all side-lobes can be
neglected).
More generally, we may plot both the magnitude and phase of the window versus frequency, as shown in Figures 3.4 and 3.5 below. In audio work, we more typically plot the window transform magnitude on a decibel (dB) scale, as shown in Fig.3.3 below. It is common to normalize the peak of the dB magnitude to 0 dB, as we have done here.
Rectangular Window Side-Lobes
From Fig.3.3 and Eq.![]() (3.4), we see that the
main-lobe width is
(3.4), we see that the
main-lobe width is
![]() radian, and the
side-lobe level is 13 dB down.
radian, and the
side-lobe level is 13 dB down.
Since the DTFT of the rectangular window approximates the
sinc
function (see (3.4)), which has an amplitude envelope
proportional to ![]() (see (3.7)), it should ``roll
off'' at approximately 6 dB per octave (since
(see (3.7)), it should ``roll
off'' at approximately 6 dB per octave (since
![]() ). This is verified in the log-log
plot of Fig.3.6.
). This is verified in the log-log
plot of Fig.3.6.
As the sampling rate approaches infinity, the rectangular window
transform (
![]() ) converges exactly to the
sinc
function.
Therefore, the departure of the roll-off from that of the
sinc
function can be ascribed to aliasing in the frequency domain,
due to sampling in the time domain (hence the name ``
) converges exactly to the
sinc
function.
Therefore, the departure of the roll-off from that of the
sinc
function can be ascribed to aliasing in the frequency domain,
due to sampling in the time domain (hence the name ``
![]() '').
'').
Note that each side lobe has width
![]() , as
measured between zero crossings.4.3 The main lobe, on the other hand, is
width
, as
measured between zero crossings.4.3 The main lobe, on the other hand, is
width ![]() . Thus, in principle, we should never confuse
side-lobe peaks with main-lobe peaks, because a peak must be at least
. Thus, in principle, we should never confuse
side-lobe peaks with main-lobe peaks, because a peak must be at least
![]() wide in order to be considered ``real''. However, in
complicated real-world scenarios, side-lobes can still cause
estimation errors (``bias''). Furthermore, two sinusoids at closely
spaced frequencies and opposite phase can partially cancel each
other's main lobes, making them appear to be narrower than
wide in order to be considered ``real''. However, in
complicated real-world scenarios, side-lobes can still cause
estimation errors (``bias''). Furthermore, two sinusoids at closely
spaced frequencies and opposite phase can partially cancel each
other's main lobes, making them appear to be narrower than
![]() .
.
In summary, the DTFT of the ![]() -sample rectangular window is
proportional to the `aliased sinc function':
-sample rectangular window is
proportional to the `aliased sinc function':
![\begin{eqnarray*}
\hbox{asinc}_M(\omega) &\isdef & \frac{\sin(\omega M / 2)}{M\cdot\sin(\omega/2)} \\ [0.2in]
&\approx& \frac{\sin(\pi fM)}{M\pi f} \isdefs \mbox{sinc}(fM)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img347.png)
Thus, it has zero crossings at integer multiples of
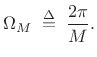 |
(4.11) |
Its main-lobe width is
Rectangular Window Summary
The rectangular window was discussed in Chapter 5 (§3.1). Here we summarize the results of that discussion.
Definition (![]() odd):
odd):
![$\displaystyle w_R(n) \isdef \left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img349.png) |
(4.12) |
Transform:
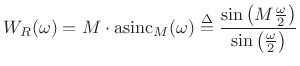 |
(4.13) |
The DTFT of a rectangular window is shown in Fig.3.7.
Properties:
- Zero crossings at integer multiples of
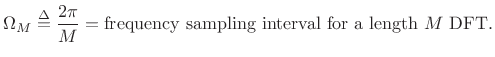
(4.14)
- Main lobe width is
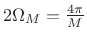 .
.
- As
 increases, the main lobe narrows (better frequency resolution).
increases, the main lobe narrows (better frequency resolution).
 has no effect on the height of the side lobes
(same as the ``Gibbs phenomenon'' for truncated Fourier series expansions).
has no effect on the height of the side lobes
(same as the ``Gibbs phenomenon'' for truncated Fourier series expansions).
- First side lobe only 13 dB down from the main-lobe peak.
- Side lobes roll off at approximately 6dB per octave.
- A phase term arises when we shift the window to make it causal, while the window transform is real in the zero-phase case (i.e., centered about time 0).
Generalized Hamming Window Family
The generalized Hamming window family is constructed by multiplying a rectangular window by one period of a cosine. The benefit of the cosine tapering is lower side-lobes. The price for this benefit is that the main-lobe doubles in width. Two well known members of the generalized Hamming family are the Hann and Hamming windows, defined below.
The basic idea of the generalized Hamming family can be seen in the
frequency-domain picture of Fig.3.8. The center dotted
waveform is the aliased sinc function
![]() (scaled rectangular window transform). The
other two dotted waveforms are scaled shifts of the same function,
(scaled rectangular window transform). The
other two dotted waveforms are scaled shifts of the same function,
![]() . The sum of all three dotted waveforms gives
the solid line. We see that
. The sum of all three dotted waveforms gives
the solid line. We see that
- there is some cancellation of the side lobes, and
- the width of the main lobe is doubled.
![\includegraphics[width=3in]{eps/shiftedSincs}](http://www.dsprelated.com/josimages_new/sasp2/img356.png) |
In terms of the rectangular window transform
![]() (the zero-phase, unit-amplitude case), this
can be written as
(the zero-phase, unit-amplitude case), this
can be written as
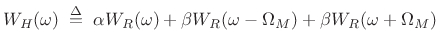 |
(4.15) |
where
Using the shift theorem (§2.3.4), we can take the inverse transform of the above equation to obtain
| (4.16) |
or,
Choosing various parameters for ![]() and
and ![]() result in
different windows in the generalized Hamming family, some of which
have names.
result in
different windows in the generalized Hamming family, some of which
have names.
Hann or Hanning or Raised Cosine
The Hann window (or hanning or raised-cosine
window) is defined based on the settings
![]() and
and ![]() in
(3.17):
in
(3.17):
where
The Hann window and its transform appear in Fig.3.9. The
Hann window can be seen as one period of a cosine ``raised'' so that
its negative peaks just touch zero (hence the alternate name ``raised cosine'').
Since it reaches zero at its endpoints with zero slope, the
discontinuity leaving the window is in the second derivative, or the
third term of its Taylor series expansion at an endpoint. As a
result, the side lobes roll off approximately 18 dB per octave. In
addition to the greatly accelerated roll-off rate, the first side lobe
has dropped from ![]() dB (rectangular-window case) down to
dB (rectangular-window case) down to ![]() dB. The main-lobe width is of course double that of the rectangular
window. For Fig.3.9, the window was computed in Matlab
as hanning(21). Therefore, it is the variant that places the
zero endpoints one-half sample to the left and right of the outermost
window samples (see next section).
dB. The main-lobe width is of course double that of the rectangular
window. For Fig.3.9, the window was computed in Matlab
as hanning(21). Therefore, it is the variant that places the
zero endpoints one-half sample to the left and right of the outermost
window samples (see next section).
Matlab for the Hann Window
In matlab, a length ![]() Hann window is designed by the statement
Hann window is designed by the statement
w = hanning(M);which, in Matlab only is equivalent to
w = .5*(1 - cos(2*pi*(1:M)'/(M+1)));For
>> hanning(3)
ans =
0.5
1
0.5
Note the curious use of M+1 in the denominator instead of
M as we would expect from the family definition in
(3.17). This perturbation serves to avoid using zero samples in
the window itself. (Why bother to multiply explicitly by zero?) Thus,
the Hann window as returned by Matlab hanning function
reaches zero one sample beyond the endpoints to the left and right.
The minus sign, which differs from (3.18), serves to make the
window causal instead of zero phase.
The Matlab Signal Processing Toolbox also includes a hann function which is defined to include the zeros at the window endpoints. For example,
>> hann(3)
ans =
0
1
0
This case is equivalent to the following matlab expression:w = .5*(1 - cos(2*pi*(0:M-1)'/(M-1)));The use of
In Matlab, both hann(3,'periodic') and hanning(3,'periodic') produce the following window:
>> hann(3,'periodic')
ans =
0
0.75
0.75
This case is equivalent to w = .5*(1 - cos(2*pi*(0:M-1)'/M));which agrees (finally) with definition (3.18). We see that in this case, the left zero endpoint is included in the window, while the one on the right lies one sample outside to the right. In general, the 'periodic' window option asks for a window that can be overlapped and added to itself at certain time displacements (
In Octave, both the hann and hanning functions include the endpoint zeros.
In practical applications, it is safest to write your own window functions in the matlab language in order to ensure portability and consistency. After all, they are typically only one line of code!
In comparing window properties below, we will speak of the Hann window
as having a main-lobe width equal to ![]() , and a side-lobe
width
, and a side-lobe
width ![]() , even though in practice they may really be
, even though in practice they may really be
![]() and
and
![]() , respectively, as illustrated
above. These remarks apply to all windows in the generalized Hamming
family, as well as the Blackman-Harris family introduced in
§3.3 below.
, respectively, as illustrated
above. These remarks apply to all windows in the generalized Hamming
family, as well as the Blackman-Harris family introduced in
§3.3 below.
Summary of Hann window properties:
- Main lobe is
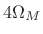 wide,
wide,
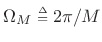
- First side lobe at -31dB
- Side lobes roll off approximately
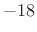 dB per octave
dB per octave
Hamming Window
The Hamming window is determined by choosing ![]() in
(3.17) (with
in
(3.17) (with
![]() ) to cancel the largest side lobe
[101].4.4 Doing this results in the values
) to cancel the largest side lobe
[101].4.4 Doing this results in the values
![\begin{eqnarray*}
\alpha &=& \frac{25}{46} \approx 0.54\\ [5pt]
\beta &=& \frac{1-\alpha}{2} \approx 0.23.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img375.png)
The peak side-lobe level is approximately ![]() dB for the Hamming
window [101].4.5 It happens that this
choice is very close to that which minimizes peak side-lobe level
(down to
dB for the Hamming
window [101].4.5 It happens that this
choice is very close to that which minimizes peak side-lobe level
(down to ![]() dB--the lowest possible within the generalized
Hamming family) [196]:
dB--the lowest possible within the generalized
Hamming family) [196]:
| (4.19) |
Since rounding the optimal
The Hamming window and its DTFT magnitude are shown in
Fig.3.10. Like the Hann window, the Hamming window is
also one period of a raised cosine. However, the cosine is raised so
high that its negative peaks are above zero, and the window has
a discontinuity in amplitude at its endpoints (stepping
discontinuously from 0.08 to 0). This makes the side-lobe roll-off
rate very slow (asymptotically ![]() dB/octave). On the other hand,
the worst-case side lobe plummets to
dB/octave). On the other hand,
the worst-case side lobe plummets to ![]() dB,4.6which is the purpose of the Hamming window. This is 10 dB better than
the Hann case of Fig.3.9 and 28 dB better than the
rectangular window. The main lobe is approximately
dB,4.6which is the purpose of the Hamming window. This is 10 dB better than
the Hann case of Fig.3.9 and 28 dB better than the
rectangular window. The main lobe is approximately ![]() wide,
as is the case for all members of the generalized Hamming family
(
wide,
as is the case for all members of the generalized Hamming family
(
![]() ).
).
Due to the step discontinuity at the window boundaries, we expect a
spectral envelope which is an aliased version of a ![]() dB per octave
(i.e., a
dB per octave
(i.e., a ![]() roll-off is converted to a ``cosecant roll-off'' by
aliasing, as derived in §3.1 and illustrated in
Fig.3.6). However, for the Hamming window, the
side-lobes nearest the main lobe have been strongly shaped by the
optimization. As a result, the nearly
roll-off is converted to a ``cosecant roll-off'' by
aliasing, as derived in §3.1 and illustrated in
Fig.3.6). However, for the Hamming window, the
side-lobes nearest the main lobe have been strongly shaped by the
optimization. As a result, the nearly ![]() dB per octave roll-off
occurs only over an interior interval of the spectrum, well between
the main lobe and half the sampling rate. This is easier to see for a
larger
dB per octave roll-off
occurs only over an interior interval of the spectrum, well between
the main lobe and half the sampling rate. This is easier to see for a
larger ![]() , as shown in
Fig.3.11, since then the optimized side-lobes nearest
the main lobe occupy a smaller frequency interval about the main
lobe.
, as shown in
Fig.3.11, since then the optimized side-lobes nearest
the main lobe occupy a smaller frequency interval about the main
lobe.
Since the Hamming window side-lobe level is more than 40 dB down, it
is often a good choice for ``1% accurate systems,'' such as 8-bit
audio signal processing systems. This is because there is rarely any
reason to require the window side lobes to lie far below the signal
quantization noise floor. The Hamming window has been extensively
used in telephone communications signal processing wherein 8-bit
CODECs were standard for many decades (albeit ![]() -law encoded).
For higher quality audio signal processing, higher quality windows may
be required, particularly when those windows act as lowpass filters
(as developed in Chapter 9).
-law encoded).
For higher quality audio signal processing, higher quality windows may
be required, particularly when those windows act as lowpass filters
(as developed in Chapter 9).
Matlab for the Hamming Window
In matlab, a length ![]() Hamming window is designed by the statement
Hamming window is designed by the statement
w = hamming(M);which is equivalent to
w = .54 - .46*cos(2*pi*(0:M-1)'/(M-1));Note that M-1 is used in the denominator rather than M+1 as in the Hann window case. Since the Hamming window cannot reach zero for any choice of samples of the defining raised cosine, it makes sense not to have M+1 here. Using M-1 (instead of M) provides that the returned window is symmetric, which is usually desired. However, we will learn later that there are times when M is really needed in the denominator (such as when the window is being used successively over time in an overlap-add scheme, in which case the sum of overlapping windows must be constant).
The hamming function in the Matlab Signal Processing Tool
Box has an optional argument 'periodic' which effectively
uses ![]() instead of
instead of ![]() . The default case is 'symmetric'.
The following examples should help clarify the difference:
. The default case is 'symmetric'.
The following examples should help clarify the difference:
>> hamming(3) % same in Matlab and Octave
ans =
0.0800
1.0000
0.0800
>> hamming(3,'symmetric') % Matlab only
ans =
0.0800
1.0000
0.0800
>> hamming(3,'periodic') % Matlab only
ans =
0.0800
0.7700
0.7700
>> hamming(4) % same in Matlab and Octave
ans =
0.0800
0.7700
0.7700
0.0800
Summary of Generalized Hamming Windows
Definition:
![$\displaystyle w_H(n) = w_R(n) \left[ \alpha + 2 \beta \cos \left( \Omega_M n \right) \right], \quad n \in {\bf Z}, \; \Omega_M \isdef \frac{2 \pi}{M}$](http://www.dsprelated.com/josimages_new/sasp2/img386.png) |
(4.20) |
where
![$\displaystyle w_R(n) \isdefs \left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img387.png) |
(4.21) |
Transform:
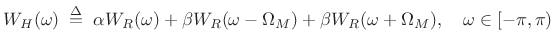 |
(4.22) |
where
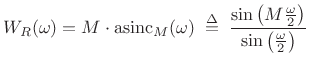 |
(4.23) |
Common Properties
- Rectangular + scaled-cosine window
- Cosine has one period across the window
- Symmetric (
 zero or linear phase)
zero or linear phase)
- Positive (by convention on
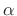 and
and  )
)
- Main lobe is
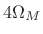 radians per sample wide, where
radians per sample wide, where

- Zero-crossings (``notches'') in window transform at intervals
of
 outside of main lobe
outside of main lobe
Figure 3.12 compares the window transforms for the rectangular, Hann, and Hamming windows. Note how the Hann window has the fastest roll-off while the Hamming window is closest to being equal-ripple. The rectangular window has the narrowest main lobe.
Rectangular window properties:
- Abrupt transition from 1 to 0 at the window endpoints
- Roll-off is asymptotically
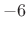 dB per octave (as
dB per octave (as
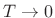 )
)
- First side lobe is
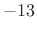 dB relative to main-lobe peak
dB relative to main-lobe peak
Hann window properties:
- Smooth transition to zero at window endpoints
- Roll-off is asymptotically -18 dB per octave
- First side lobe is
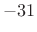 dB relative to main-lobe peak
dB relative to main-lobe peak
Hamming window properties:
- Discontinuous ``slam to zero'' at endpoints
- Roll-off is asymptotically -6 dB per octave
- Side lobes are closer to ``equal ripple''
- First side lobe is
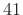 dB down =
dB down = 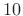 dB better than
Hann4.7
dB better than
Hann4.7
The MLT Sine Window
The modulated lapped transform (MLT) [160] uses the sine window, defined by
![$\displaystyle w(n) = \sin\left[\left(n+\frac{1}{2}\right)\frac{\pi}{2M}\right], \quad n=0,1,2,\ldots,2M-1\,.$](http://www.dsprelated.com/josimages_new/sasp2/img398.png) |
(4.24) |
The sine window is used in MPEG-1, Layer 3 (MP3 format), MPEG-2 AAC, and MPEG-4 [200].
Properties:
- Side lobes 24 dB down
- Asymptotically optimal coding gain [159]
- Zero-phase-window transform (``truncated cosine window'')
has smallest moment of inertia over all windows [202]:
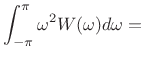 min
min(4.25)
Note that in perceptual audio coding systems, there is both an
analysis window and a synthesis window. That is, the
sine window is deployed twice, first when encoding the signal,
and second when decoding. As a result, the sine window is
squared in practical usage, rendering it equivalent to a Hann
window (![]() ) in the final output signal (when there are no
spectral modifications).
) in the final output signal (when there are no
spectral modifications).
It is of great practical value that the second window application occurs after spectral modifications (such as spectral quantization); any distortions due to spectral modifications are tapered gracefully to zero by the synthesis window. Synthesis windows were introduced at least as early as 1980 [213,49], and they became practical for audio coding with the advent of time-domain aliasing cancellation (TDAC) [214]. The TDAC technique made it possible to use windows with 50% overlap without suffering a doubling of the number of samples in the short-time Fourier transform. TDAC was generalized to ``lapped orthogonal transforms'' (LOT) by Malvar [160]. The modulated lapped transform (MLT) is a variant of LOT used in conjunction with the modulated discrete cosine transform (MDCT) [160]. See also [287] and [291].
Blackman-Harris Window Family
The Blackman-Harris (BH) window family is a straightforward generalization of the Hamming family introduced in §3.2. Recall from that discussion that the generalized Hamming family was constructed using a summation of three shifted and scaled aliased-sinc-functions (shown in Fig.3.8). The Blackman-Harris family is obtained by adding still more shifted sinc functions:
where
 , and
, and 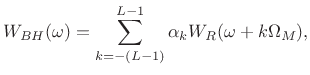 |
(4.27) |
where
Note that for ![]() , we obtain the rectangular window, and for
, we obtain the rectangular window, and for ![]() ,
the BH family specializes to the generalized Hamming family.
,
the BH family specializes to the generalized Hamming family.
Blackman Window Family
When ![]() in (3.26), we obtain the Blackman family:
in (3.26), we obtain the Blackman family:
| (4.28) |
Relative to the generalized Hamming family (§3.2), we have added one more cosine weighted by
Classic Blackman
The so-called ``Blackman Window'' is the specific case for which
![]()
![]() , and
, and
![]() . It has
the following properties:
. It has
the following properties:
- Side lobes roll off at about
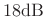 per octave (like Hann)
per octave (like Hann)
- Side-lobe level is about
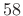 dB (worst case)
dB (worst case)
- One degree of freedom used to increase the roll-off rate from 6dB/octave (like rectangular) to 18 dB per octave by matching amplitude and slope to 0 at the window endpoints
- One degree of freedom is used to minimize side lobes (like Hamming)
- One degree of freedom is used to scale the window
Matlab for the Classic Blackman Window
N = 101; L = 3; No2 = (N-1)/2; n=-No2:No2; ws = zeros(L,3*N); z = zeros(1,N); for l=0:L-1 ws(l+1,:) = [z,cos(l*2*pi*n/N),z]; end alpha = [0.42,0.5,0.08]; % Classic Blackman w = alpha * ws;
Figure 3.13 plots the classic Blackman Window and its transform.
Three-Term Blackman-Harris Window
The classic Blackman window of the previous section is a three-term
window in the Blackman-Harris family (![]() ), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
-
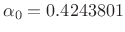
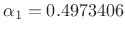 , and
, and
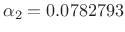 .
.
- Side-lobe level
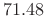 dB
dB
- Side lobes roll off
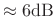 per octave in the absence of aliasing
(like rectangular and Hamming)
per octave in the absence of aliasing
(like rectangular and Hamming)
- All degrees of freedom (scaling aside) are used to minimize side lobes (like Hamming)
Figure 3.14 plots the three-term Blackman-Harris Window and its transform. Figure 3.15 shows the same display for a much longer window of the same type, to illustrate its similarity to the rectangular window (and Hamming window) at high frequencies.
Frequency-Domain Implementation of the
Blackman-Harris Family
The Blackman-Harris window family can be very efficiently implemented
in the frequency domain as a ![]() -point convolution with the
spectrum of the unwindowed data.
-point convolution with the
spectrum of the unwindowed data.
For example, to implement a zero-phase Hann window,
- Start with a length
 rectangular window
rectangular window
- Take an
 -point DFT
-point DFT
- Convolve the DFT data with the 3-point smoother
![$ W=[1/4,1/2,1/4]$](http://www.dsprelated.com/josimages_new/sasp2/img423.png)
Similarly, any Blackman window may be implemented as a 5-point
smoother in the frequency domain. More generally, any ![]() -term
Blackman-Harris window requires convolution of the critically sampled
spectrum with a smoother of length
-term
Blackman-Harris window requires convolution of the critically sampled
spectrum with a smoother of length ![]() .
.
Power-of-Cosine Window Family
Definition:
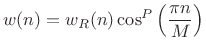 |
(4.29) |
where
Properties:
- The first
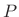 terms of the window's Taylor expansion, evaluated at the endpoints are identically 0
.
terms of the window's Taylor expansion, evaluated at the endpoints are identically 0
.
- Roll-off rate
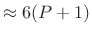 dB/octave.
dB/octave.
Special Cases:
-
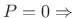 Rectangular window
Rectangular window
-
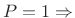 MLT sine window
MLT sine window
-
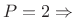 Hann window (``raised cosine'' = ``
Hann window (``raised cosine'' = ``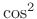 '')
'')
-
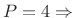 Alternative Blackman (maximized roll-off rate)
Alternative Blackman (maximized roll-off rate)
Thus, ![]() windows parametrize
windows parametrize ![]() -term Blackman-Harris windows
(for
-term Blackman-Harris windows
(for ![]() ) which are configured to use all degrees-of-freedom to
maximize roll-off rate.
) which are configured to use all degrees-of-freedom to
maximize roll-off rate.
Spectrum Analysis of an Oboe Tone
In this section we compare three FFT windows applied to an oboe recording. The examples demonstrate that more gracefully tapered windows support a larger spectral dynamic range, at the cost of reduced frequency resolution.
Rectangular-Windowed Oboe Recording
Figure 3.16a shows a segment of two quasi periods from an oboe recording at the pitch C4, and Fig.3.16b shows the corresponding FFT magnitude. The window length was set to the next integer greater than twice the period length in samples. The FFT size was set to the next power of 2 which was at least five times the window length (for a minimum zero-padding factor of 5). The complete Matlab script is listed in §F.2.5.
![\includegraphics[width=\twidth]{eps/oboeboxcar}](http://www.dsprelated.com/josimages_new/sasp2/img433.png) |
Hamming-Windowed Oboe Recording
Figure 3.17a shows a segment of four quasi periods from the same oboe recording as in the previous figure multiplied by a Hamming window, and Fig.3.17b shows the corresponding zero-padded FFT magnitude. Note how the lower side-lobes of the Hamming window significantly improve the visibility of spectral components above 6 kHz or so.
![\includegraphics[width=\twidth]{eps/oboehamming}](http://www.dsprelated.com/josimages_new/sasp2/img434.png) |
Blackman-Windowed Oboe Recording
Figure 3.18a shows a segment of six quasi periods from the same oboe recording as in Fig.3.16 multiplied by a Blackman window, and Fig.3.18b shows the corresponding zero-padded FFT magnitude data. The lower side lobes of the Blackman window significantly improve over the Hamming-window results at high frequencies.
![\includegraphics[width=\twidth]{eps/oboeblackman}](http://www.dsprelated.com/josimages_new/sasp2/img435.png) |
Conclusions
In summary, only the Blackman window clearly revealed all of the oboe harmonics. This is because the spectral dynamic range of signal exceeded that of the window transform in the case of rectangular and Hamming windows. In other words, the side lobes corresponding to the loudest low-frequency harmonics were comparable to or louder than the signal harmonics at high frequencies.
Note that preemphasis (flattening the spectral envelope using a
preemphasis filter) would have helped here by reducing the spectral
dynamic range of the signal (see §10.3 for a number of
methods). In voice signal processing, approximately ![]() dB/octave
preemphasis is common because voice spectra generally roll off at
dB/octave
preemphasis is common because voice spectra generally roll off at ![]() dB per octave [162]. If
dB per octave [162]. If ![]() denotes the original voice
spectrum and
denotes the original voice
spectrum and
![]() the preemphasized spectrum, then one method
is to use a ``leaky first-order difference''
the preemphasized spectrum, then one method
is to use a ``leaky first-order difference''
| (4.30) |
For voice signals, the preemphasized spectrum
Bartlett (``Triangular'') Window
The Bartlett window (or simply triangular window) may be defined by
![$\displaystyle w(n) = w_R(n)\left[1 - \frac{\vert n\vert}{\frac{M-1}{2}}\right], \quad n\in\left[-\frac{M-1}{2},\frac{M-1}{2}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img442.png) |
(4.31) |
and the corresponding transform is
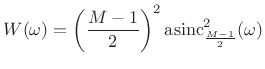 |
(4.32) |
The following properties are immediate:
- Convolution of two length
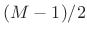 rectangular windows
rectangular windows
- Main lobe twice as wide as that of a rectangular window of length

- First side lobe twice as far down as rectangular case (-26 dB)
- Often applied implicitly to sample correlations of finite data
- Also called the ``tent function''
- Can replace
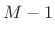 by
by 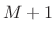 to avoid including endpoint zeros
to avoid including endpoint zeros
Matlab for the Bartlett Window:
In matlab, a length ![]() Bartlett window is designed by the statement
Bartlett window is designed by the statement
w = bartlett(M);This is equivalent, for odd
w = 2*(0:(M-1)/2)/(M-1); w = [w w((M-1)/2:-1:1)]';Note that, in contrast to the hanning function, but like the hann function, bartlett explicitly includes zeros at its endpoints:
>> bartlett(3)
ans =
0
1
0
The triang function in Matlab implements the triangular
window corresponding to the hanning case:
>> triang(3)
ans =
0.5000
1.0000
0.5000
Poisson Window
The Poisson window (or more generically exponential window) can be written
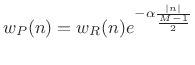 |
(4.33) |
where
 |
(4.34) |
where
The Poisson window is plotted in Fig.3.19. In the ![]() plane, the Poisson window has the effect of radially contracting
the unit circle. Consider an infinitely long Poisson window
(no truncation by a rectangular window
plane, the Poisson window has the effect of radially contracting
the unit circle. Consider an infinitely long Poisson window
(no truncation by a rectangular window ![]() ) applied to a causal
signal
) applied to a causal
signal ![]() having
having ![]() transform
transform ![]() :
:
![\begin{eqnarray*}
H_P(z) &=& \sum_{n=0}^\infty [w(n)h(n)] z^{-n} \\
&=& \sum_{n=0}^\infty \left[h(n) e^{- \frac{ \alpha n}{ M/2 }}\right] z^{-n}
\qquad\hbox{(let $r\isdef e^{-\frac{\alpha}{ M/2 }}$)}\\
&=& \sum_{n=0}^\infty h(n) z^{-n} r^{n}
= \sum_{n=0}^\infty h(n) (z/r)^{-n} \\
&=& H\left(\frac{z}{r}\right)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img450.png)
Thus, the unit-circle response is moved to ![]() . This means, for
example, that marginally stable poles in
. This means, for
example, that marginally stable poles in ![]() now decay as
now decay as
![]() in
in ![]() .
.
The effect of this radial ![]() -plane contraction is shown in Fig.3.20.
-plane contraction is shown in Fig.3.20.
The Poisson window can be useful for impulse-response modeling by poles and/or zeros (``system identification''). In such applications, the window length is best chosen to include substantially all of the impulse-response data.
Hann-Poisson Window
Definition:
![$\displaystyle w(n) = \frac{1}{2}\left[1 + \cos\left(\pi\frac{n}{\frac{M-1}{2}}\right)\right] e^{-\alpha\frac{\vert n\vert}{\frac{M-1}{2}}}$](http://www.dsprelated.com/josimages_new/sasp2/img455.png) |
(4.35) |
![\includegraphics[width=\twidth]{eps/hannPoissonWindow}](http://www.dsprelated.com/josimages_new/sasp2/img456.png) |
The Hann-Poisson window is, naturally enough, a Hann window times a Poisson window (exponential times raised cosine). It is plotted along with its DTFT in Fig.3.21.
The Hann-Poisson window has the very unusual feature among windows of
having ``no side lobes'' in the sense that, for
![]() , the
window-transform magnitude has negative slope for all positive
frequencies [58], as shown in
Fig.3.22. As a result, this window is valuable for
``hill climbing'' optimization methods such as Newton's method or any
convex optimization methods. In other terms, of all windows we have
seen so far, only the Hann-Poisson window has a
convex transform magnitude to the left or right of the peak
(Fig.3.21b).
, the
window-transform magnitude has negative slope for all positive
frequencies [58], as shown in
Fig.3.22. As a result, this window is valuable for
``hill climbing'' optimization methods such as Newton's method or any
convex optimization methods. In other terms, of all windows we have
seen so far, only the Hann-Poisson window has a
convex transform magnitude to the left or right of the peak
(Fig.3.21b).
Figure 3.23 also shows the slope and curvature of the Hann-Poisson
window transform, but this time with ![]() increased to 3. We see
that higher
increased to 3. We see
that higher ![]() further smooths the side lobes, and even the
curvature becomes uniformly positive over a broad center range.
further smooths the side lobes, and even the
curvature becomes uniformly positive over a broad center range.
Matlab for the Hann-Poisson Window
function [w,h,p] = hannpoisson(M,alpha) %HANNPOISSON - Length M Hann-Poisson window Mo2 = (M-1)/2; n=(-Mo2:Mo2)'; scl = alpha / Mo2; p = exp(-scl*abs(n)); scl2 = pi / Mo2; h = 0.5*(1+cos(scl2*n)); w = p.*h;
Slepian or DPSS Window
A window having maximal energy concentration in the main lobe is given
by the digital prolate spheroidal sequence (DPSS) of order 0
[256,136]. It is obtained by using
all ![]() degrees of freedom (sample values) in an
degrees of freedom (sample values) in an ![]() -point
window
-point
window ![]() to obtain a window transform
to obtain a window transform
![]() which maximizes the energy in the
main lobe of the window relative to total energy:
which maximizes the energy in the
main lobe of the window relative to total energy:
In the continuous-time case, i.e., when
A prolate spheroidal wave function is defined as an eigenfunction of the integral equation
where
![\begin{eqnarray*}
&& [\hbox{\sc Chop}_{2\omega_c}(W)]*[D\,\mbox{sinc}(D\omega)]\\
&=& \hbox{\sc FT}(\hbox{\sc Chop}_D(\hbox{\sc IFT}(\hbox{\sc Chop}_{2\omega_c}(W)))) \eqsp \lambda W
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img468.png)
where
![]() is a rectangular windowing operation which zeros
is a rectangular windowing operation which zeros
![]() outside the interval
outside the interval
![]() .
.
Satisfying (3.37) means that window transform ![]() is an eigenfunction of this sequence of operations; that is, it can be
zeroed outside the interval
is an eigenfunction of this sequence of operations; that is, it can be
zeroed outside the interval
![]() , inverse Fourier
transformed, zeroed outside the interval
, inverse Fourier
transformed, zeroed outside the interval
![]() , and forward
Fourier transformed to yield the original Window transform
, and forward
Fourier transformed to yield the original Window transform ![]() multiplied by some scale factor
multiplied by some scale factor ![]() (the eigenvalue of the
overall operation). We may say that
(the eigenvalue of the
overall operation). We may say that ![]() is the bandlimited
extrapolation of its main lobe.
is the bandlimited
extrapolation of its main lobe.
The sinc function in (3.37) can be regarded as a
symmetric Toeplitz operator kernel), and the integral
of ![]() multiplied by this kernel can be called a symmetric
Toeplitz operator. This is a special case of a Hermitian operator,
and by the general theory of Hermitian operators, there exists an
infinite set of mutually orthogonal functions
multiplied by this kernel can be called a symmetric
Toeplitz operator. This is a special case of a Hermitian operator,
and by the general theory of Hermitian operators, there exists an
infinite set of mutually orthogonal functions
![]() , each
associated with a real eigenvalues
, each
associated with a real eigenvalues ![]() .4.9 If
.4.9 If
![]() denotes the largest such eigenvalue of (3.37),
then its corresponding eigenfunction,
denotes the largest such eigenvalue of (3.37),
then its corresponding eigenfunction,
![]() , is what we want as our Slepian window, or
prolate spheroidal window in the continuous-time case. It is
optimal in the sense of having maximum main-lobe energy as a fraction
of total energy.
, is what we want as our Slepian window, or
prolate spheroidal window in the continuous-time case. It is
optimal in the sense of having maximum main-lobe energy as a fraction
of total energy.
The discrete-time counterpart is Digital Prolate Spheroidal Sequences (DPSS), which may be defined as the eigenvectors of the following symmetric Toeplitz matrix constructed from a sampled sinc function [13]:
![$\displaystyle S[k,l] = \frac{\sin[\omega_c T(k-l)]}{k-l}, \quad k,l=0,1,2,\ldots,M-1$](http://www.dsprelated.com/josimages_new/sasp2/img478.png) |
(4.38) |
where
Matlab for the DPSS Window
The function dpss in the Matlab Signal Processing Tool Box4.10 can be used to compute them as follows:
w = dpss(M,alpha,1); % discrete prolate spheroidal sequencewhere
Some examples of DPSS windows and window transforms are given in Fig.3.29.
Kaiser Window
Jim Kaiser discovered a simple approximation to the DPSS window based upon Bessel functions [115], generally known as the Kaiser window (or Kaiser-Bessel window).
Definition:
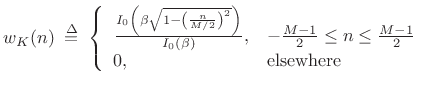 |
(4.39) |
Window transform:
The Fourier transform of the Kaiser window ![]() (where
(where ![]() is
treated as continuous) is given by4.11
is
treated as continuous) is given by4.11
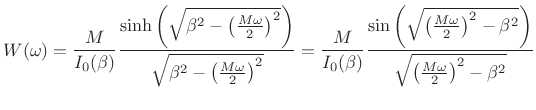 |
(4.40) |
where
![$\displaystyle I_0(x) \isdefs \sum_{k=0}^{\infty} \left[ \frac{\left(\frac{x}{2}\right)^k}{k!} \right]^2
$](http://www.dsprelated.com/josimages_new/sasp2/img489.png)
Notes:
- Reduces to rectangular window for
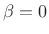
- Asymptotic roll-off is 6 dB/octave
- First null in window transform is at
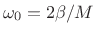
- Time-bandwidth product
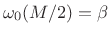 radians
if bandwidths are measured from 0 to positive band-limit
radians
if bandwidths are measured from 0 to positive band-limit
- Full time-bandwidth product
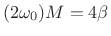 radians
when frequency bandwidth is defined as main-lobe width
out to first null
radians
when frequency bandwidth is defined as main-lobe width
out to first null
- Sometimes the Kaiser window is parametrized by
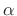 , where
, where
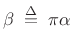
(4.42)
Kaiser Window Beta Parameter
The ![]() parameter of the Kaiser window provides a convenient
continuous control over the fundamental window trade-off between
side-lobe level and main-lobe width. Larger
parameter of the Kaiser window provides a convenient
continuous control over the fundamental window trade-off between
side-lobe level and main-lobe width. Larger ![]() values give lower
side-lobe levels, but at the price of a wider main lobe. As discussed
in §5.4.1, widening the main lobe reduces
frequency resolution when the window is used for spectrum
analysis. As explored in Chapter 9, reducing the side lobes reduces ``channel cross
talk'' in an FFT-based filter-bank implementation.
values give lower
side-lobe levels, but at the price of a wider main lobe. As discussed
in §5.4.1, widening the main lobe reduces
frequency resolution when the window is used for spectrum
analysis. As explored in Chapter 9, reducing the side lobes reduces ``channel cross
talk'' in an FFT-based filter-bank implementation.
The Kaiser beta parameter can be interpreted as 1/4 of the
``time-bandwidth product''
![]() of the window
in radians (seconds times radians-per-second).4.13 Sometimes the Kaiser window is
parametrized by
of the window
in radians (seconds times radians-per-second).4.13 Sometimes the Kaiser window is
parametrized by
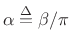 instead of
instead of ![]() . The
. The
![]() parameter is therefore half the window's time-bandwidth
product
parameter is therefore half the window's time-bandwidth
product
![]() in cycles (seconds times
cycles-per-second).
in cycles (seconds times
cycles-per-second).
Kaiser Windows and Transforms
Figure 3.24 plots the Kaiser window and its transform for
![]() . Note how increasing
. Note how increasing ![]() causes the
side-lobes to fall away from the main lobe. The curvature at the main
lobe peak also decreases somewhat.
causes the
side-lobes to fall away from the main lobe. The curvature at the main
lobe peak also decreases somewhat.
Figure 3.25 shows a plot of the Kaiser window
for various values of
![]() . Note that for
. Note that for ![]() , the
Kaiser window reduces to the rectangular window.
, the
Kaiser window reduces to the rectangular window.
Figure 3.26 shows a plot of the Kaiser window
transforms for
![]() . For
. For ![]() (top plot),
we see the dB magnitude of the aliased sinc function. As
(top plot),
we see the dB magnitude of the aliased sinc function. As ![]() increases the main-lobe widens and the side lobes go lower, reaching
almost 50 dB down for
increases the main-lobe widens and the side lobes go lower, reaching
almost 50 dB down for ![]() .
.
Figure 3.27 shows the effect of increasing window length
for the Kaiser window. The window lengths are
![]() from the top to the bottom plot. As with all windows, increasing the
length decreases the main-lobe width, while the side-lobe level
remains essentially unchanged.
from the top to the bottom plot. As with all windows, increasing the
length decreases the main-lobe width, while the side-lobe level
remains essentially unchanged.
Figure 3.28 shows a plot of the Kaiser window side-lobe level
for various values of
![]() . For
. For
![]() , the Kaiser window reduces to the rectangular window, and we
expect the side-lobe level to be about 13 dB below the main lobe
(upper-lefthand corner of Fig.3.28). As
, the Kaiser window reduces to the rectangular window, and we
expect the side-lobe level to be about 13 dB below the main lobe
(upper-lefthand corner of Fig.3.28). As
![]() increases, the dB side-lobe level reduces approximately linearly with
main-lobe width increase (approximately a 25 dB drop in side-lobe
level for each main-lobe width increase by one sinc-main-lobe).
increases, the dB side-lobe level reduces approximately linearly with
main-lobe width increase (approximately a 25 dB drop in side-lobe
level for each main-lobe width increase by one sinc-main-lobe).
Minimum Frequency Separation vs. Window Length
The requirements on window length for resolving closely tuned
sinusoids was discussed in §5.5.2. This section considers
this issue for the Kaiser window. Table 3.1 lists the ![]() parameter required for a Kaiser window to resolve equal-amplitude
sinusoids with a frequency spacing of
parameter required for a Kaiser window to resolve equal-amplitude
sinusoids with a frequency spacing of
![]() rad/sample
[1, Table 8-9]. Recall from §3.9 that
rad/sample
[1, Table 8-9]. Recall from §3.9 that
![]() can be interpreted as half of the time-bandwidth of the
window (in cycles).
can be interpreted as half of the time-bandwidth of the
window (in cycles).
|
Kaiser and DPSS Windows Compared
Figure 3.29 shows an overlay of DPSS and Kaiser windows
for some different ![]() values. In all cases, the window length
was
values. In all cases, the window length
was ![]() . Note how the two windows become more similar as
. Note how the two windows become more similar as ![]() increases. The Matlab for computing the windows is as follows:
increases. The Matlab for computing the windows is as follows:
w1 = dpss(M,alpha,1); % discrete prolate spheroidal seq. w2 = kaiser(M,alpha*pi); % corresponding kaiser window
The following Matlab comparison of the DPSS and Kaiser windows
illustrates the interpretation of ![]() as the bin number of the
edge of the critically sampled window main lobe, i.e., when the DFT
length equals the window length:
as the bin number of the
edge of the critically sampled window main lobe, i.e., when the DFT
length equals the window length:
format long; M=17; alpha=5; abs(fft([ dpss(M,alpha,1), kaiser(M,pi*alpha)/2])) ans = 2.82707022360190 2.50908747431366 2.00652719015325 1.92930705688346 0.68469697658600 0.85272343521683 0.09415916813555 0.19546670371747 0.00311639169878 0.01773139505899 0.00000050775691 0.00022611995322 0.00000003737279 0.00000123787805 0.00000000262633 0.00000066206722 0.00000007448708 0.00000034793207 0.00000007448708 0.00000034793207 0.00000000262633 0.00000066206722 0.00000003737279 0.00000123787805 0.00000050775691 0.00022611995322 0.00311639169878 0.01773139505899 0.09415916813555 0.19546670371747 0.68469697658600 0.85272343521683 2.00652719015325 1.92930705688346
Finally, Fig.3.30 shows a comparison of DPSS and Kaiser window transforms, where the DPSS window was computed using the simple method listed in §F.1.2. We see that the DPSS window has a slightly narrower main lobe and lower overall side-lobe levels, although its side lobes are higher far from the main lobe. Thus, the DPSS window has slightly better overall specifications, while Kaiser-window side lobes have a steeper roll off.
Dolph-Chebyshev Window
The Dolph-Chebyshev Window (or Chebyshev window, or
Dolph window) minimizes the Chebyshev norm of the side
lobes for a given main-lobe width ![]() [61,101],
[224, p. 94]:
[61,101],
[224, p. 94]:
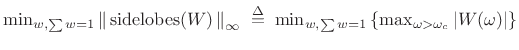 |
(4.43) |
The Chebyshev norm is also called the
An equivalent formulation is to minimize main-lobe width subject to a side-lobe specification:
 |
(4.44) |
The optimal Dolph-Chebyshev window transform can be written in closed form [61,101,105,156]:
![\begin{eqnarray*}
W(\omega_k) &=& \frac{\cos\left\{M\cos^{-1}\left[\beta\cos\left(\frac{\pi k}{M}\right)
\right]\right\}}{\cosh\left[M\cosh^{-1} (\beta)\right]},
\qquad k=0,1,2,\ldots,M-1 \\
\beta &=& \cosh \left[\frac{1}{M}\cosh^{-1}(10^\alpha)\right], \qquad (\alpha\approx 2,3,4).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img520.png)
The zero-phase Dolph-Chebyshev window, ![]() , is then computed as the
inverse DFT of
, is then computed as the
inverse DFT of
![]() .4.14 The
.4.14 The ![]() parameter controls the side-lobe level via the formula [156]
parameter controls the side-lobe level via the formula [156]
| Side-Lobe Level in dB |
(4.45) |
Thus,
The Chebyshev window can be regarded as the impulse response of an optimal Chebyshev lowpass filter having a zero-width pass-band (i.e., the main lobe consists of two ``transition bands''--see Chapter 4 regarding FIR filter design more generally).
Matlab for the Dolph-Chebyshev Window
In Matlab, the function chebwin(M,ripple) computes a length
![]() Dolph-Chebyshev window having a side-lobe level ripple dB below
that of the main-lobe peak. For example,
Dolph-Chebyshev window having a side-lobe level ripple dB below
that of the main-lobe peak. For example,
w = chebwin(31,60);designs a length
Example Chebyshev Windows and Transforms
Figure 3.31 shows the Dolph-Chebyshev window and its transform as designed by chebwin(31,40) in Matlab, and Fig.3.32 shows the same thing for chebwin(31,200). As can be seen from these examples, higher side-lobe levels are associated with a narrower main lobe and more discontinuous endpoints.
Figure 3.33 shows the Dolph-Chebyshev window and its transform as designed by chebwin(101,40) in Matlab. Note how the endpoints have actually become impulsive for the longer window length. The Hamming window, in contrast, is constrained to be monotonic away from its center in the time domain.
The ``equal ripple'' property in the frequency domain perfectly satisfies worst-case side-lobe specifications. However, it has the potentially unfortunate consequence of introducing ``impulses'' at the window endpoints. Such impulses can be the source of ``pre-echo'' or ``post-echo'' distortion which are time-domain effects not reflected in a simple side-lobe level specification. This is a good lesson in the importance of choosing the right error criterion to minimize. In this case, to avoid impulse endpoints, we might add a continuity or monotonicity constraint in the time domain (see §3.13.2 for examples).
Chebyshev and Hamming Windows Compared
Figure 3.34 shows an overlay of Hamming and Dolph-Chebyshev window transforms,
the ripple parameter for chebwin set to ![]() dB to make it
comparable to the Hamming side-lobe level. We see that the
monotonicity constraint inherent in the Hamming window family only
costs a few dB of deviation from optimality in the Chebyshev sense at
high frequency.
dB to make it
comparable to the Hamming side-lobe level. We see that the
monotonicity constraint inherent in the Hamming window family only
costs a few dB of deviation from optimality in the Chebyshev sense at
high frequency.
Dolph-Chebyshev Window Theory
In this section, the main elements of the theory behind the Dolph-Chebyshev window are summarized.
Chebyshev Polynomials
The ![]() th Chebyshev polynomial may be defined by
th Chebyshev polynomial may be defined by
![$\displaystyle T_n(x) = \left\{\begin{array}{ll} \cos[n\cos^{-1}(x)], & \vert x\vert\le1 \\ [5pt] \cosh[n\cosh^{-1}(x)], & \vert x\vert>1 \\ \end{array} \right..$](http://www.dsprelated.com/josimages_new/sasp2/img534.png) |
(4.46) |
The first three even-order cases are plotted in Fig.3.35. (We will only need the even orders for making Chebyshev windows, as only they are symmetric about time 0.) Clearly,
| (4.47) |
for
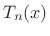 is an
is an  th-order polynomial in
th-order polynomial in  .
.
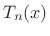 is an even function when
is an even function when  is an even integer,
and odd when
is an even integer,
and odd when  is odd.
is odd.
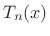 has
has  zeros in the open interval
zeros in the open interval 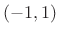 , and
, and
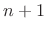 extrema in the closed interval
extrema in the closed interval ![$ [-1,1]$](http://www.dsprelated.com/josimages_new/sasp2/img543.png) .
.
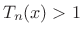 for
for 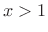 .
.
Dolph-Chebyshev Window Definition
Let ![]() denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
![$\displaystyle W(\omega) = \frac{T_{M-1}[x_0 \cos(\omega/2)]}{T_{M-1}(x_0)}$](http://www.dsprelated.com/josimages_new/sasp2/img546.png) |
(4.48) |
where
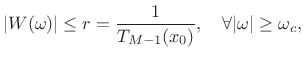 |
(4.49) |
where
![$\displaystyle \omega_c \isdefs 2\cos^{-1}\left[\frac{1}{x_0}\right].$](http://www.dsprelated.com/josimages_new/sasp2/img549.png) |
(4.50) |
Expanding
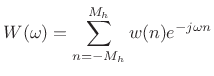 |
(4.51) |
where
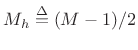 . Thus, the coefficients
. Thus, the coefficients
Dolph-Chebyshev Window Main-Lobe Width
Given the window length ![]() and ripple magnitude
and ripple magnitude ![]() , the main-lobe
width
, the main-lobe
width ![]() may be computed as follows [155]:
may be computed as follows [155]:
![\begin{eqnarray*}
x_0 &=& \cosh\left[\frac{\cosh^{-1}\left(\frac{1}{r}\right)}{M-1}\right]\\
\omega_c &=& 2\cos^{-1}\left(\frac{1}{x_0}\right)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img553.png)
This is the smallest main-lobe width possible for the given window length and side-lobe spec.
Dolph-Chebyshev Window Length Computation
Given a prescribed side-lobe ripple-magnitude ![]() and main-lobe width
and main-lobe width
![]() , the required window length
, the required window length ![]() is given by [155]
is given by [155]
![$\displaystyle M = 1 + \frac{\cosh^{-1}(1/r)}{\cosh^{-1}[\sec(\omega_c/2)]}.$](http://www.dsprelated.com/josimages_new/sasp2/img554.png) |
(4.52) |
For
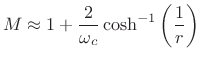 |
(4.53) |
Thus, half the time-bandwidth product in radians is approximately
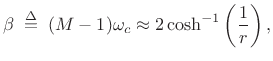 |
(4.54) |
where
Gaussian Window and Transform
The Gaussian ``bell curve'' is possibly the only smooth, nonzero function, known in closed form, that transforms to itself.4.15
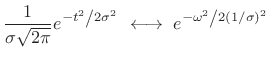 |
(4.55) |
It also achieves the minimum time-bandwidth product
| (4.56) |
when ``width'' is defined as the square root of its second central moment. For even functions
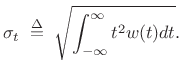 |
(4.57) |
Since the true Gaussian function has infinite duration, in practice we must window it with some usual finite window, or truncate it.
Depalle [58] suggests using a
triangular window raised to some power ![]() for this
purpose, which preserves the absence of side lobes for
sufficiently large
for this
purpose, which preserves the absence of side lobes for
sufficiently large ![]() . It also preserves non-negativity
of the transform.
. It also preserves non-negativity
of the transform.
Matlab for the Gaussian Window
In matlab, w = gausswin(M,alpha) returns a length ![]() window
with parameter
window
with parameter
![]() where
where
![]() is defined, as in Harris
[101], so that the window shape is invariant with respect to
window length
is defined, as in Harris
[101], so that the window shape is invariant with respect to
window length ![]() :
:
function [w] = gausswin(M,alpha) n = -(M-1)/2 : (M-1)/2; w = exp((-1/2) * (alpha * n/((M-1)/2)) .^ 2)';
An implementation in terms of unnormalized standard deviation (sigma in samples) is as follows:
function [w] = gaussianwin(M,sigma) n= -(M-1)/2 : (M-1)/2; w = exp(-n .* n / (2 * sigma * sigma))';In this case, sigma would normally be specified as a fraction of the window length
Note that, on a dB scale, Gaussians are quadratic. This means that parabolic interpolation of a sampled Gaussian transform is exact. This can be a useful fact to remember when estimating sinusoidal peak frequencies in spectra. For example, one suggested implication is that, for typical windows, quadratic interpolation of spectral peaks may be more accurate on a log-magnitude scale (e.g., dB) than on a linear magnitude scale (this has been observed empirically for a variety of cases).
Gaussian Window and Transform
Figure 3.36 shows an example length ![]() Gaussian window
and its transform. The sigma parameter was set to
Gaussian window
and its transform. The sigma parameter was set to ![]() so that
simple truncation of the Gaussian yields a side-lobe level better than
so that
simple truncation of the Gaussian yields a side-lobe level better than
![]() dB. Also overlaid on the window transform is a parabola; we see
that the main lobe is well fit by the parabola until the side lobes
begin. Since the transform of a Gaussian is a Gaussian (exactly), the
side lobes are entirely caused by truncating the window.
dB. Also overlaid on the window transform is a parabola; we see
that the main lobe is well fit by the parabola until the side lobes
begin. Since the transform of a Gaussian is a Gaussian (exactly), the
side lobes are entirely caused by truncating the window.
More properties and applications of the Gaussian function can be found in Appendix D.
Exact Discrete Gaussian Window
It can be shown [44] that
| (4.58) |
where
Optimized Windows
We close this chapter with a general discussion of optimal windows in a wider sense. We generally desire
| (4.59) |
but the nature of this approximation is typically determined by characteristics of audio perception. Best results are usually obtained by formulating this as an FIR filter design problem (see Chapter 4). In general, both time-domain and frequency-domain specifications are needed. (Recall the potentially problematic impulses in the Dolph-Chebyshev window shown in Fig.3.33 when its length was long and ripple level was high). Equivalently, both magnitude and phase specifications are necessary in the frequency domain.
A window transform can generally be regarded as the frequency response
of a lowpass filter having a stop band corresponding to
the side lobes and a pass band corresponding to the main lobe
(or central section of the main lobe). Optimal lowpass filters
require a transition region from the pass band to the stop
band. For spectrum analysis windows, it is natural to define the
entire main lobe as ``transition region.'' That is, the
pass-band width is zero. Alternatively, the pass-band could be
allowed to have a finite width, allowing some amount of ``ripple'' in
the pass band; in this case, the pass-band ripple will normally be
maximum at the main-lobe midpoint (
![]() , say), and at the
pass-band edges (
, say), and at the
pass-band edges (
![]() ). By
embedding the window design problem within the more general problem of
FIR digital filter design, a plethora of optimal design techniques can
be brought to bear
[204,258,14,176,218].
). By
embedding the window design problem within the more general problem of
FIR digital filter design, a plethora of optimal design techniques can
be brought to bear
[204,258,14,176,218].
Optimal Windows for Audio Coding
Recently, numerically optimized windows have been developed by Dolby which achieve the following objectives:
- Narrow the window in time
- Smooth the onset and decay in time
- Reduce side lobes below the worst-case masking threshold
See §4.10 for an overview of optimal methods for FIR digital filter design.
General Rule
There is rarely a closed form expression for the optimal window in
practice. The most important task is to formulate an ideal
error criterion. Given the right error criterion, it is usually
straightforward to minimize it numerically with respect to the window
samples ![]() .
.
Window Design by Linear Programming
This section, based on a class project by EE graduate student Tatsuki Kashitani, illustrates the use of linprog in Matlab for designing variations on the Chebyshev window (§3.10). In addition, some comparisons between standard linear programming and the Remez exchange algorithm (firpm) are noted.
Linear Programming (LP)
If we can get our filter or window design problems in the form
![\begin{displaymath}\begin{array}[t]{ll} \mathrm{minimize} & f^{T}x\\ \mathrm{subject}\, \mathrm{to} & \begin{array}[t]{l} \mathbf{A}_{eq}x=b_{eq}\\ \mathbf{A}x\le b\end{array}, \end{array}\end{displaymath}](http://www.dsprelated.com/josimages_new/sasp2/img581.png) |
(4.60) |
where
The linprog function in Matlab Optimization Toolbox solves LP problems. In Octave, one can use glpk instead (from the GNU GLPK library).
LP Formulation of Chebyshev Window Design
What we want:
- Symmetric zero-phase window.
- Window samples to be positive.
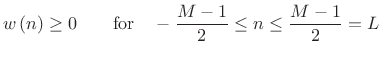
(4.61)
- Transform to be 1 at DC.
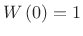
(4.62)
- Transform to be within
![$ \left[-\delta ,\delta \right]$](http://www.dsprelated.com/josimages_new/sasp2/img588.png) in the stop-band.
in the stop-band.
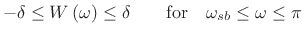
(4.63)
- And
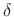 to be small.
to be small.
Symmetric Window Constraint
Because we are designing a zero-phase window, use only the
positive-time part
![]() :
:
| (4.64) |
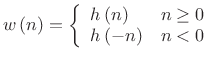 |
(4.65) |
Positive Window-Sample Constraint
For each window sample,
![]() , or,
, or,
| (4.66) |
Stacking inequalities for all
![$\displaystyle \left[\begin{array}{ccccc} -1 & 0 & \cdots & 0 & 0\\ 0 & -1 & & & 0\\ \vdots & & \ddots & & \vdots \\ 0 & & & -1 & 0\\ 0 & 0 & \cdots & 0 & -1\end{array} \right]\left[\begin{array}{c} h\left(0\right)\\ h\left(1\right)\\ \vdots \\ h\left(L-1\right)\\ h\left(L\right)\end{array} \right] \le \left[\begin{array}{c} 0\\ 0\\ \vdots \\ 0\\ 0 \end{array} \right]$](http://www.dsprelated.com/josimages_new/sasp2/img596.png) |
(4.67) |
or
| (4.68) |
DC Constraint
The DTFT at frequency ![]() is given by
is given by
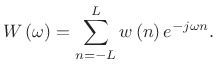 |
(4.69) |
By zero-phase symmetry,
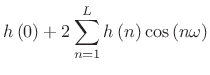 |
|||
![$\displaystyle \left[\begin{array}{cccc}
1 & 2\cos \left(\omega \right) & \cdots & 2\cos \left(L\omega \right)\end{array}\right]\left[\begin{array}{c}
h\left(0\right)\\
h\left(1\right)\\
\vdots \\
h\left(L\right)\end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img601.png) |
|||
So
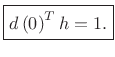 |
(4.70) |
Sidelobe Specification
Likewise, side-lobe specification can be enforced at frequencies
![]() in the stop-band.
in the stop-band.
| (4.71) |
or
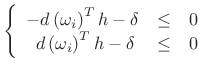 |
(4.72) |
where
| (4.73) |
We need
![$\displaystyle \left[\begin{array}{c}
-d\left(\omega _1\right)^{T}\\
\vdots \\
-d\left(\omega _{K}\right)^{T}\\
d\left(\omega _1\right)^{T}\\
\vdots \\
d\left(\omega _{K}\right)^{T}\end{array}\right]h+\left[\begin{array}{c}
-\delta \\
\vdots \\
-\delta \\
-\delta \\
\vdots \\
-\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img610.png) |
|||
![$\displaystyle \left[\begin{array}{cc}
-d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
-d\left(\omega _{K}\right)^{T} & -1\\
d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
d\left(\omega _{K}\right)^{T} & -1
\end{array}\right]\left[\begin{array}{c}
h\\
\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img613.png) |
I.e.,
![$\displaystyle \zbox {\mathbf{A}_{sb}\left[\begin{array}{c} h\\ \delta \end{array} \right] \le \mathbf{0}.}$](http://www.dsprelated.com/josimages_new/sasp2/img615.png) |
(4.74) |
LP Standard Form
Now gather all of the constraints to form an LP problem:
![\begin{displaymath}\begin{array}[t]{ll} \mathrm{minimize} & \left[\begin{array}{cccc} 0 & \cdots & 0 & 1\end{array} \right] \left[\begin{array}{c} h\\ \delta \end{array} \right]\\ [5pt] \mbox{subject to} & \begin{array}[t]{l} \left[\begin{array}{cc} d\left(0\right)^{T} & 0\end{array} \right]\left[\begin{array}{c} h\\ \delta \end{array} \right]=1\\ \left[\begin{array}{c} \left[\begin{array}{cc} -\mathbf{I} & \mathbf{0}\end{array} \right]\\ [5pt] \mathbf{A}_{sb}\end{array} \right]\left[\begin{array}{c} h\\ \delta \end{array} \right]\le \mathbf{0}\end{array} \end{array}\end{displaymath}](http://www.dsprelated.com/josimages_new/sasp2/img616.png) |
(4.75) |
where the optimization variables are
Solving this linear-programming problem should produce a window that is optimal in the Chebyshev sense over the chosen frequency samples, as shown in Fig.3.37. If the chosen frequency samples happen to include all of the extremal frequencies (frequencies of maximum error in the DTFT of the window), then the unique Chebyshev window for the specified main-lobe width must be obtained. Iterating to find the extremal frequencies is the heart of the Remez multiple exchange algorithm, discussed in the next section.
Remez Exchange Algorithm
The Remez multiple exchange algorithm works by moving the frequency samples each iteration to points of maximum error (on a denser grid). Remez iterations could be added to our formulation as well. The Remez multiple exchange algorithm (function firpm [formerly remez] in the Matlab Signal Processing Toolbox, and still remez in Octave) is normally faster than a linear programming formulation, which can be regarded as a single exchange method [224, p. 140]. Another reason for the speed of firpm is that it solves the following equations non-iteratively for the filter exhibiting the desired error alternation over the current set of extremal frequencies:
![$\displaystyle \left[ \begin{array}{c} H(\omega_1) \\ H(\omega_2) \\ \vdots \\ H(\omega_{K}) \end{array} \right] = \left[ \begin{array}{cccccc} 1 & 2\cos(\omega_1) & \dots & 2\cos(\omega_1L) & \frac{1}{W(\omega_1)} \\ 1 & 2\cos(\omega_2) & \dots & 2\cos(\omega_2L) & \frac{-1}{W(\omega_2)} \\ \vdots & & & \\ 1 & 2\cos(\omega_{K}) & \dots & 2\cos(\omega_{K}L) & \frac{(-1)^{K}}{W(\omega_{K})} \end{array} \right] \left[ \begin{array}{c} h_0 \\ h_1 \\ \vdots \\ h_{L} \\ \delta \end{array} \right]$](http://www.dsprelated.com/josimages_new/sasp2/img619.png) |
(4.76) |
where
Convergence of Remez Exchange
According to a theorem of Remez, ![]() is guaranteed to
increase monotonically each iteration, ultimately converging to
its optimal value. This value is reached when all the extremal
frequencies are found. In practice, numerical round-off error may
cause
is guaranteed to
increase monotonically each iteration, ultimately converging to
its optimal value. This value is reached when all the extremal
frequencies are found. In practice, numerical round-off error may
cause ![]() not to increase monotonically. When this is detected,
the algorithm normally halts and reports a failure to converge.
Convergence failure is common in practice for FIR filters having more
than 300 or so taps and stringent design specifications (such as very
narrow pass-bands). Further details on Remez exchange are given
in [224, p. 136].
not to increase monotonically. When this is detected,
the algorithm normally halts and reports a failure to converge.
Convergence failure is common in practice for FIR filters having more
than 300 or so taps and stringent design specifications (such as very
narrow pass-bands). Further details on Remez exchange are given
in [224, p. 136].
As a result of the non-iterative internal LP solution on each iteration, firpm cannot be used when additional constraints are added, such as those to be discussed in the following sections. In such cases, a more general LP solver such as linprog must be used. Recent advances in convex optimization enable faster solution of much larger problems [22].
Monotonicity Constraint
We can constrain the positive-time part of the window to be monotonically decreasing:
| (4.77) |
In matrix form,
![$\displaystyle \left[\begin{array}{ccccc}
-1 & 1 & & & 0\\
& -1 & 1 & & \\
& & \ddots & \ddots & \\
0 & & & -1 & 1\end{array}\right]h$](http://www.dsprelated.com/josimages_new/sasp2/img623.png) |
or,
| (4.78) |
See Fig.3.38.
L-Infinity Norm of Derivative Objective
We can add a smoothness objective by adding
![]() -norm of the
derivative to the objective function.
-norm of the
derivative to the objective function.
| (4.79) |
The
![]() -norm only cares about the maximum derivative.
Large
-norm only cares about the maximum derivative.
Large ![]() means we put more weight on the smoothness than the
side-lobe level.
means we put more weight on the smoothness than the
side-lobe level.
This can be formulated as an LP by adding one optimization parameter
![]() which bounds all derivatives.
which bounds all derivatives.
| (4.80) |
In matrix form,
![$\displaystyle \left[\begin{array}{r}
-\mathbf{D}\\
\mathbf{D}\end{array}\right]h-\sigma \mathbf1$](http://www.dsprelated.com/josimages_new/sasp2/img631.png) |
Objective function becomes
| (4.81) |
The result of adding the Chebyshev norm of diff(h) to the
objective function to be minimized (![]() ) is shown in
Fig.3.39. The result of increasing
) is shown in
Fig.3.39. The result of increasing ![]() to 20 is
shown in Fig.3.40.
to 20 is
shown in Fig.3.40.
L-One Norm of Derivative Objective
Another way to add smoothness constraint is to add ![]() -norm of
the derivative to the objective:
-norm of
the derivative to the objective:
| (4.82) |
Note that the
We can formulate an LP problem by adding a vector of optimization
parameters ![]() which bound derivatives:
which bound derivatives:
| (4.83) |
In matrix form,
![$\displaystyle \left[\begin{array}{r} -\mathbf{D}\\ \mathbf{D}\end{array} \right]h-\left[\begin{array}{c} -\tau \\ -\tau \end{array} \right]\le 0.$](http://www.dsprelated.com/josimages_new/sasp2/img638.png) |
(4.84) |
The objective function becomes
| (4.85) |
See Fig.3.41 and Fig.3.42 for example results.
Summary
This section illustrated the design of optimal spectrum-analysis windows made using linear-programming (linprog in matlab) or Remez multiple exchange algorithms (firpm in Matlab). After formulating the Chebyshev window as a linear programming problem, we found we could impose a monotonicity constraint on its shape in the time domain, or various derivative constraints. In Chapter 4, we will look at methods for FIR filter design, including the window method (§4.5) which designs FIR filters as a windowed ideal impulse response. The formulation introduced in this section can be used to design such windows, and it can be used to design optimal FIR filters. In such cases, the impulse response is designed directly (as the window was here) to minimize an error criterion subject to various equality and inequality constraints, as discussed above for window design.4.16
Next Section:
FIR Digital Filter Design
Previous Section:
Fourier Transforms for Continuous/Discrete Time/Frequency








![\includegraphics[width=3.5in]{eps/rectWindow}](http://www.dsprelated.com/josimages_new/sasp2/img306.png)
![$\displaystyle \frac{e^{-j \omega \frac{1}{2}}}{e^{-j\omega \frac{1}{2}}}
\left[ \frac{ e^{j \omega \frac{M}{2}}-e^{-j\omega\frac{M}{2}}}
{e^{j \omega\frac{1}{2}}-e^{-j\omega\frac{1}{2}}} \right]$](http://www.dsprelated.com/josimages_new/sasp2/img311.png)
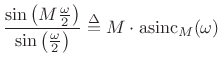
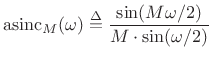
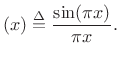
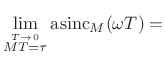 sinc
sinc![\includegraphics[width=\textwidth ,height=2.25in]{eps/rectWindowRawFT}](http://www.dsprelated.com/josimages_new/sasp2/img329.png)
![\includegraphics[width=\twidth]{eps/rectWindowFT}](http://www.dsprelated.com/josimages_new/sasp2/img334.png)
![% latex2html id marker 73365
\includegraphics[width=\twidth,height=0.3125\theight]{eps/rectWindowFTzeroX}](http://www.dsprelated.com/josimages_new/sasp2/img335.png)
![% latex2html id marker 73369
\includegraphics[width=\twidth,height=0.3125\theight]{eps/rectWindowPhaseFT}](http://www.dsprelated.com/josimages_new/sasp2/img336.png)
![\includegraphics[width=\textwidth ]{eps/rectWindowLLFT}](http://www.dsprelated.com/josimages_new/sasp2/img341.png)
![\includegraphics[width=\twidth]{eps/Rect}](http://www.dsprelated.com/josimages_new/sasp2/img351.png)
![$\displaystyle \zbox {w_H(n) = w_R(n) \left[ \alpha + 2 \beta \cos \left( \frac{2 \pi n}{M} \right) \right].} \protect$](http://www.dsprelated.com/josimages_new/sasp2/img361.png)
![$\displaystyle w_H(n)=w_R(n) \left[ \frac{1}{2} + \frac{1}{2} \cos( \Omega_M n) \right] = w_R(n) \cos^2\left(\frac{\Omega_M}{2} n\right) \protect$](http://www.dsprelated.com/josimages_new/sasp2/img362.png)
![\includegraphics[width=4in]{eps/hanningWindow}](http://www.dsprelated.com/josimages_new/sasp2/img365.png)
![\includegraphics[width=\twidth]{eps/hammingWindow}](http://www.dsprelated.com/josimages_new/sasp2/img381.png)
![\includegraphics[width=\twidth]{eps/hammingWindowLong}](http://www.dsprelated.com/josimages_new/sasp2/img384.png)
![\includegraphics[width=\twidth]{eps/RectHannHamm}](http://www.dsprelated.com/josimages_new/sasp2/img392.png)
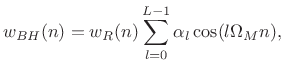
![\includegraphics[width=\twidth]{eps/blackmanWindow}](http://www.dsprelated.com/josimages_new/sasp2/img414.png)
![\includegraphics[width=\twidth]{eps/blackmanHarris3}](http://www.dsprelated.com/josimages_new/sasp2/img420.png)
![\includegraphics[width=\twidth]{eps/blackmanHarris3Long}](http://www.dsprelated.com/josimages_new/sasp2/img421.png)
![\includegraphics[width=3.5in]{eps/poissonwindow}](http://www.dsprelated.com/josimages_new/sasp2/img447.png)
![\includegraphics[width=3.5in]{eps/zplane2}](http://www.dsprelated.com/josimages_new/sasp2/img454.png)
![\includegraphics[width=\twidth]{eps/hannPoissonSlope}](http://www.dsprelated.com/josimages_new/sasp2/img458.png)
![\includegraphics[width=\twidth]{eps/hannPoissonSlope2}](http://www.dsprelated.com/josimages_new/sasp2/img459.png)
![$\displaystyle \max_w \left[ \frac{ \mbox{main lobe energy} } { \mbox{total energy} } \right] \protect$](http://www.dsprelated.com/josimages_new/sasp2/img462.png)
![$\displaystyle \int_{-\omega_c}^{\omega_c} W(\nu) \frac{\sin[\pi D\cdot(\omega-\nu)]}{\pi(\omega-\nu)}\, d\omega = \lambda W(\omega) \protect$](http://www.dsprelated.com/josimages_new/sasp2/img465.png)
![\includegraphics[width=\twidth]{eps/kaiser123}](http://www.dsprelated.com/josimages_new/sasp2/img499.png)
![\includegraphics[width=\twidth]{eps/KaiserTBetas}](http://www.dsprelated.com/josimages_new/sasp2/img501.png)
![\includegraphics[width=\twidth]{eps/KaiserFBetas}](http://www.dsprelated.com/josimages_new/sasp2/img504.png)
![\includegraphics[width=\twidth]{eps/KaiserFLengths}](http://www.dsprelated.com/josimages_new/sasp2/img506.png)
![\includegraphics[width=\twidth]{eps/kaiserBeta}](http://www.dsprelated.com/josimages_new/sasp2/img508.png)
![\includegraphics[width=\twidth]{eps/dpsstest}](http://www.dsprelated.com/josimages_new/sasp2/img515.png)
![\includegraphics[width=\twidth]{eps/dpsskaiser-fd}](http://www.dsprelated.com/josimages_new/sasp2/img516.png)
![\includegraphics[width=\twidth]{eps/cheb31R40}](http://www.dsprelated.com/josimages_new/sasp2/img528.png)
![\includegraphics[width=\twidth]{eps/cheb31R200}](http://www.dsprelated.com/josimages_new/sasp2/img529.png)
![\includegraphics[width=\twidth]{eps/cheb101R40}](http://www.dsprelated.com/josimages_new/sasp2/img530.png)
![\begin{psfrags}
% latex2html id marker 9837\psfrag{freq}{$\omega T$\ (radians per sample)}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/chebHammingC}
\caption{}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img532.png)
![\includegraphics[width=\twidth]{eps/first-even-chebs-c}](http://www.dsprelated.com/josimages_new/sasp2/img533.png)
![\includegraphics[width=\twidth]{eps/gaussianWindow}](http://www.dsprelated.com/josimages_new/sasp2/img573.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_normal_chebwin}](http://www.dsprelated.com/josimages_new/sasp2/img618.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_monotonic_chebwin}](http://www.dsprelated.com/josimages_new/sasp2/img626.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_linf_chebwin_1}](http://www.dsprelated.com/josimages_new/sasp2/img634.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_linf_chebwin_2}](http://www.dsprelated.com/josimages_new/sasp2/img635.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_lone_chebwin_1}](http://www.dsprelated.com/josimages_new/sasp2/img640.png)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_lone_chebwin_2}](http://www.dsprelated.com/josimages_new/sasp2/img641.png)











