Spectral Flipping Around Signal Center Frequency

• Tips and Tricks
• Multirate DSP

Most of us are familiar with the process of flipping the spectrum (spectral inversion) of a real signal by multiplying that signal's time samples by (-1)ⁿ. In that process the center of spectral rotation is f_s/4, where f_s is the signal's sample rate in Hz. In this blog we discuss a different kind of spectral flipping process.

Consider the situation where we need to flip the X(f) spectrum in Figure 1(a) to obtain the desired Y(f) spectrum shown in Figure 1(b). Notice that the center of rotation of the desired spectral flipping is not f_s /4, but is instead the signal's f_cntr center frequency. The simple spectral flipping process of multiplying a signal's time samples by (-1)ⁿ does not solve our problem because that process would result in the undesirable spectrum shown in Figure 1(c).

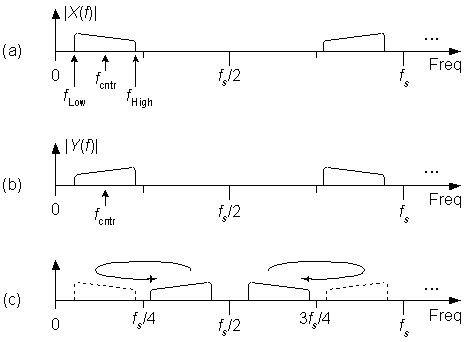
       Figure 1: Spectral flipping, centered at f_cntr: (a) original spectrum ranging from f_Low to f_High; (b) desired spectrum; (c) incorrect spectrum.

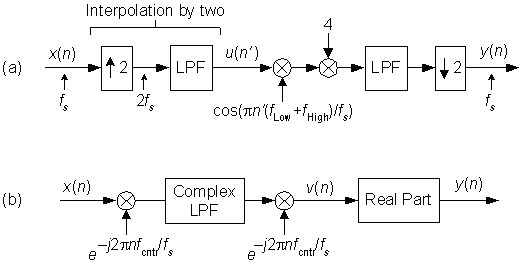
There are two methods to solve our f_cntr-centered spectral flipping problem. Figure 2(a) shows the first method, comprising a multirate processing technique. In considering this spectral flipping method, we should keep in mind that:

* The two identical lowpass filters have passbands that extend from zero Hz to f_High Hz. (Note that the sample rate for both filters is 2f_s Hz.)

* The cosine mixing sequence uses the upsampled-by-two time index variable n'.

* The multiply by four operation compensates for the sequence u(n') amplitude loss by a factor of two caused by interpolation, and the amplitude loss by another factor of two due to the cosine mixing.

Of course, a clever engineer will eliminate the multiply by four operation altogether by increasing the DC (zero Hz) gain of one of the lowpass filters by four.

The second method we could use to obtain a signal having the desired Figure 1(b) spectrum is the neat process shown in Figure 2(b), suggested by Dirk Bell [1]. While somewhat more computationally intensive than the above multirate method, this technique works well and deserves mention here. In this second method, as Bell recommends, we can combine the last two stages of the process (the complex multiply and the Real Part extraction) by computing only the real part of sequence v(n) yielding our desired y(n).

References:

[1] Bell, D. "Subject: Re: Frequency Inversion", Usenet group comp.dsp post, Aug. 30, 2006.

Copyright © 2007, Richard Lyons, All Rights Reserved

Sign in