Frequency Dependence in Free Space Propagation

• Basics
• Wireless
• Communication

Introduction

It seems to be fairly common knowledge, even among practicing professionals, that the efficiency of propagation of wireless signals is frequency dependent. Generally it is believed that lower frequencies are desirable since pathloss effects will be less than they would be at higher frequencies. As evidence of this, the Friis Transmission Equation[i] is often cited, the general form of which is usually written as:

P_r = P_t G_t G_r ( λ / 4πd )² (1)

where the (λ/4πd)² term is sometimes referred to as the path loss or free space loss. The following definitions are assumed:

P_r - The received signal power.

P_t - The transmitted signal power.

G_r - The gain of the receiving antenna.

G_t - The gain of the transmitting antenna.

λ - The wavelength of the carrier (i.e., the center frequency of the radiated signal)

d - The distance between the transmitting and receiving antennas.

It is evident from Equation (1) that, all other variables held constant, as the transmission frequency is reduced, the wavelength, λ, increases. The received power, P_r, then goes up by the square of the wavelength! Clearly it is always desirable to use as low a frequency as possible, correct?

Well, not really.

At least it's evident that propagation is frequency dependent!

Uh, no.

I am often surprised at the number and stature of engineers and researchers in the wireless industry who believe this to be true, though. So why is there so much confusion around this? Is the Friis equation incorrect? What's happening to our young people these days, anyway? Okay, we'll skip that last one, but we can address the first two, and learn why the propagation of an electromagnetic wave in free space is generally and practically completely independent of frequency[ii].

What is "Propagation"?

One source of confusion is what is meant by "propagation". For the purposes of this discussion, and in order to fully illuminate the root of the issue, it is good to get a better understanding of what is meant by "channel effects" and "propagation effects". A "channel" is generally, and I'll take a little license here, the medium through which a given set of information is conveyed. In a wireless system this usually includes what I call "the propagation channel" as well as "the radio channel". The "propagation channel" includes things like path loss, multipath reflection effects, multipath fading, Doppler (which can also be induced by moving reflectors in the environment, even if the radio terminals are stationary), fading due to material penetration (e.g., wall penetration, cloud penetration, etc.), etc., etc. For the most part, I think of the "propagation channel" as what happens to the signal between the antennas, and for applications like mobile radio or Non-Line-of-Sight links "propagation channel" effects can dominate the impairments and distortion that the demodulator must handle in order to recover the transmitted information. The terminology of "channel effects" is a bit broader, and includes "propagation effects" but also adds what I call "radio channel" effects, or the effects of the antennas, signal cabling, filter distortions, amplifier distortions and nonlinearities, amplifier noise, mixing distortions, quantization noise, etc., etc. The idea is to capture pretty much any distortion or impairment that happens to the signal from the point that it is "modulated" into a signal and the point at which is it "demodulated" back into the estimate of the original transmitted information. This includes imperfections in signal processing and radio components.

Other impairment effects, like interference from other signals, may be lumped into "propagation effects" even though they do not affect the physical propagation of the electromagnetic wave carrying the signal. Even by my definition, that "propagation effects" are what happens between the antennas, one would have to include interference since an interference source could easily be, and often is, between the transmit and receive antennas.

Another important issue is whether or not the antenna itself is included when discussing "propagation", and this winds up being a key point, if not the key point. Antenna response and antenna design generally is highly frequency dependent, but the propagation of an electromagnetic wave in free space is not. So whether or not one means to include antennas in a discussion regarding "propagation" makes all the difference in the world.

So it's not hard to see why there is often disagreement or just misunderstanding regarding where the "radio effects" start and stop and where the "propagation effects" take over, and whether or not "propagation" includes antennas or not, or interference or not, blah blah blah. The immediate point is not to sort all that out, but just to understand that there are significant sources of the confusion and that they're pretty common. It is very rare that a speaker, or standard, or proposal, or text book[iii], clarifies this distinction. Many times this may be because that level of detail is inappropriate for the particular discussion, or the clarification too peripheral to the main point, or because the source is also unaware of the confusion or distinction.

Gaining Knowledge About Antennas

Anybody who's spent much time with an antenna designer knows that there's a fair amount of art involved in the process. There are important fine details and mysterious field effects, material properties, planetary alignments and other things beyond the understanding of mere mortals that have significant influences on antenna behavior. Fortunately, for the purposes of our discussion here, we can leave the padlocks safely secure on the doors that separate the antenna designers from the rest of society. The aspects of antenna behavior that come into play for understanding the fundamentals of frequency dependence are pretty basic, enough so that I think even I can take a crack at explaining them well enough to get to the point.

Consider a point radiator that emanates a certain amount of power, P, equally in all directions, i.e., the ideal omnidirectional antenna. The area covered by the antenna radiation in free space at a distance, d, from the radiator is just the area of a sphere, A_sphere = 4πd². As the distance from the radiator increases, the area covered increases with the square of the distance. We can say that the power flux density decreases with the square of the distance. A common intuitive example to help imagine this is the inflation of a balloon, perhaps with a small square drawn on the surface. As the balloon is inflated the skin of the balloon gets thinner as it has to cover more area, which is demonstrated by the increasing area of the square as the radius of the balloon increases. The power flux density of the transmitted signal likewise grows thinner with distance, and the recoverable power within a given area drops by the square of the distance.

All antennas have an area metric called the Effective Area or Effective Aperture, usually denoted as A_e, which describes the antenna's ability to collect power. Continuing with the radiating sphere example, since the power flux density from an omnidirectional radiator can be computed from the distance, the Effective Area of an antenna can be determined by measuring the amount of power collected at given distance from an omnidirectional radiation of P power, or in a given power flux density. So, in simple terms, A_e is the ratio of the collected power to the power flux density incident upon it. The effective area may or may not have much to do with or correlate well with the physical dimensions of the antenna. It is merely an indicator of the power collection ability of the device.

So the amount of power collected at a receiving antenna with effective area A_er from an ideal omnidirectional radiator transmitting P_t power is, strictly from the geometric relationship:

P_r = P_t A_er / 4πd² (2)

Note that there is no frequency dependence in the relationship shown in (2). The only variables that affect the amount of power received are the propagation distance, d, the transmitted power, P_t, and the effective area of the receiving antenna. Equation (2) can be generalized for a non-omnidirectional transmit antenna by substituting the Effective Isotropic Radiated Power (EIRP) for the total transmit omnidirectional transmit power, P_t. Since the basic concept of EIRP is to quantify the power flux density independent of the gain or configuration of the transmit antenna, this is a useful step in further generalizing the relationship, so that

P_r = EIRP A_er / 4πd² (3)

Again, we note that there is still no frequency dependence expressed in Equation (3) regardless of what type of antennas are used.

Since Equations (2) and (3) suggest that the propagation of the electromagnetic waves have no frequency dependence, there is clearly some factor in play that introduces the wavelength term, λ, into Eq. (1). To understand this we need only to look closely at the common expression for antenna gain, specifically

G = 4πA_e / λ² (4)

Equation (4) can be found in many texts on communications, electromagnetics, or antennas[iv]. It is given here without background for brevity.[v]

There are several things we can learn from Equation (4), and we don't even need to delve far into the details of antenna theory or design. Let's consider breaking Eq. (4) into two separate cases: omnidirectional radiators, specifically monopole or dipole antennas, and directive reflecting antennas, commonly referred to as "dish" antennas.

In the omnidirectional, dipole or monopole, case, we know that the size of the antenna needs to be matched to the frequency of operation for maximum efficiency. Generally a stub element in a monopole antenna is cut to a quarter-wavelength of the desired operating frequency, and a dipole consists of two such quarter-wave stubs butted up against each other as shown in Figure 1. Since this means that the physical size of the antenna gets smaller when optimized for a particular higher frequency, this has an effect on the antenna's ability to collect energy. Setting G = 1 in Eq. (4), as would be the case for an omnidirectional radiator, we see that

A_e = λ² / 4π (5)

which reveals that, sure enough, the effective area, A_e, increases with the square of the wavelength, so that lower frequencies provide a substantial advantage in energy collection. This is not difficult to understand intuitively; dipole or monopole antennas get physically larger when sized for lower frequencies. It is this characteristic, that an omnidirectional stick antenna's effective area increases when physically dimensioned for lower frequencies, that misleads many people into believing that "propagation" is frequency dependent.

We should be careful to understand, though, that this effect relates to stick antennas that are physically dimensioned to a particular frequency, e.g., monopoles cut to quarter-wavelengths. A given antenna will exhibit frequency selectivity in that it will have a bandpass characteristic related to the resonating efficiency of the particular design. Generally dipole or monopole antennas have well-behaved bandpass characteristics that can cover bands of interest with reasonable efficiency. For any given stick antenna, then, the only frequency dependence has to do with the particular bandpass frequency selectivity of the design, and one expects a monopole or dipole to have a peak response matched to the quarter-wavelength related to the physical size of the antenna. Figure 2 illustrates the "frequency dependence" shown in Eq. (5) compared to typical responses of stick antennas at various frequencies.

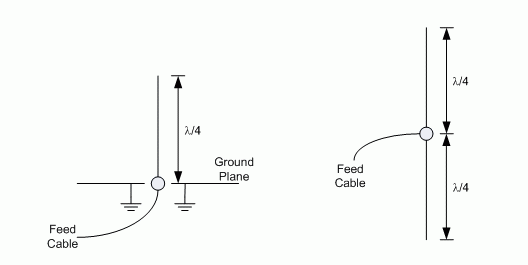
Figure 1. A monopole (left) and dipole (right) antenna, with the quarter-wavelength dimensions shown.

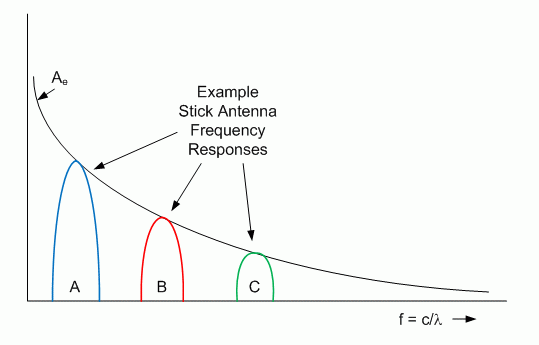
Figure 2. The effective area, A_e, of a stick antenna, with the dimensions shown in Figure 1, increases with the square of the wavelength. Individual antennas cut to specific frequencies, like those shown as A, B, and C, will generally have bandpass frequency selectivity.

For the reflecting dish antenna case the physical size of the antenna also plays a revealing part in illuminating the mystery of frequency dependent propagation. We can see in Equation (4) that if we desire to build a high-gain (i.e., high-G) antenna, we can increase A_e or we can decrease the wavelength, λ. For a reflecting dish of a given size, A_e will be fixed by the dimensions of the device, but the gain will increase with frequency. Again we see a frequency dependence related to the antenna but in the opposite sense of the omnidirectional stick antenna case. Instead of a loss with increasing frequency, we see antenna gain improving with the square of the frequency.

Closing the Link Between Antennas and Frequency Dependence

Now that we understand that the type of antenna has a significant effect on the "frequency dependence" of propagation, let's take another look at the Friis Transmission Equation. It is not difficult to start from Equations (2) or (3) and (4) and derive Equation (1). Along the way one might stumble across the point which we will now attempt to make.

The general form of the equation shown in Eq. (1) is convenient when the gains of the transmit and receive antennas are known. If we assume that both the transmit and receive antennas are unity-gain, omnidirectional stick antennas, i.e., G_t = G_r = 1, then we have

P_r = P_t λ² / 4πd² (6)

Eq. (6) is not at all surprising, since we already sorted out that stick antennas gain effectiveness, in the form of increased effective area, proportional to λ². Again, the "frequency dependence" in Eq. (6) has to do with the physical dimensioning of a stick antenna to match the desired wavelength, and not the actual propagation of the wave through space. If someone were to apply Eq. (6) to a link with a carrier at a particular wavelength but antennas dimensioned for a different frequency, they might spend a fair amount of time trying to reconcile the discrepancy if they were unaware of the basis for the wavelength term in the equation.

Likewise if we have a dish antenna at each end of the link, both with fixed dimensions and therefore fixed effective areas, we could substitute Eq (4) into Eq (1) and write

P_r = P_t A_et A_er / λ²d² (7)

Again, we experience no surprise that λ has moved from the numerator in (6) to the denominator in (7), since we've already determined that reflective dish antennas of fixed area experience a gain improvement proportional to the square of the frequency. We also know that Eq (7) is not in contradiction to Eq (1) or Eq (6), and is essentially a recognizable form of Eq (3).

We can now anticipate the inevitable combination of fixed gain omnidirectional and fixed area reflecting antenna and write

P_r = P_t G_t A_er / 4πd² (8)

or the simple rearrangement switching the forms of the transmit and receive antennas

P_r = P_t A_et G_r / 4πd² (9)

As expected, in these cases the "frequency dependent" characteristics of the antennas cancel and there is no longer a frequency-related term in Equations (8) or (9) at all. This helps demonstrate to those who may remain skeptical that the wavelength term in the Friis Transmission equation has to do with the antennas and not the actual propagation of the wave through space.

What This Doesn't Mean

The Friis equation, in the various forms we are now familiar with, addresses link behavior in free space. We now understand that free space propagation between the antennas is completely independent of frequency. An important caveat, though, is that many links have something other than free space between the antennas. The propagation of a wave from a fixed broadcast tower to a receiver inside a house or building must penetrate the roof, walls, windows, doors, tree leaves, or whatever materials lie in the path between the transmitter and receiver. It is very often the case that a wave must penetrate various materials on its way to whatever receiving antennas it may encounter.

It is well known and generally true that material penetration is frequency dependent, and generally attenuation increases with frequency. That is, the higher the frequency of the wave the more opaque that materials appear to be. Since the type and thickness of the material makes a difference in the amount of attenuation experienced, consideration of penetration losses is a much more complicated endeavor than the free space analysis that we've just done. So while material penetration loss generally increases with frequency, specific cases and scenarios require detailed analysis suitable for the particular application.

Some materials exhibit substantial attenuation properties at particular frequencies and less attenuation at frequencies above or below their resonance band. A notable example is the oxygen absorption bands around 60GHz. The range of radio waves at these frequencies is decreased significantly by the energy absorption of atmospheric oxygen molecules.

Summary, Conclusion, and Chest-Beating

It is apparent from careful study of the Friis Transmission Equation that the often-mentioned "frequency-dependent propagation loss" of radio waves is really an antenna effect and not a wave propagation effect. The propagation of a radio wave or photon through free space is unaffected by its frequency. Stick antennas, that is, dipole or monopole antennas, are larger at lower frequencies and therefore have more effective area for energy collection. Reflective antennas, that is dish antennas, of a given size have higher gain with decreasing wavelength. Systems that use stick antennas therefore benefit from lower frequencies while dish-antenna systems will attain higher system gain at higher frequencies.

Remember to use this knowledge for good and not for evil, although it should be possible to impress smug colleagues if the topic ever comes up.

References:

[1] Bernard Sklar, Digital Communications, Prentice-Hall, Englewood Cliffs, NJ, 1988

[2] D.K. Cheng, Field and Wave Electromagnetics, Addison-Wesley, 1983

[i] Sometimes called the Friis Range Equation or other suitably creative names.

[ii] There are some arguable exceptions in the extreme cases, if you tilt your head just right. For example, quantum background noise increases substantially above about 70GHz. This does not effect "propagation" in that it does not impede a wave or photon, but it does interfere with its detection in a receiver.

[iii] Sklar's text, [1], is a notable exception. See Section 4.3.3, p. 200.

[iv] Cheng's text, [2], has a nice, basic derivation of (4). See Section 11-6.2, p. 531. I'm sure other texts have good treatments as well.

[v] Not that brevity is a strong suit of mine.

Copyright © 2008, Eric Jacobsen, All Rights Reserved.

Sign in