DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Complex Example

To illustrate an example involving complex poles, consider the filter

$\displaystyle H(z) \eqsp \frac{g}{1+z^{-2}}, $

where $ g$ can be any real or complex value. (When $ g$ is real, the filter as a whole is real also.) The poles are then $ p_1=j$ and $ p_2=-j$ (or vice versa), and the factored form can be written as

$\displaystyle H(z) \eqsp \frac{g}{(1-jz^{-1})(1+jz^{-1})}. $

Using Eq.$ \,$(6.8), the residues are found to be

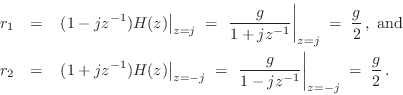
\begin{eqnarray*} r_1 &=& \left.(1-jz^{-1})H(z)\right\vert _{z=j} \eqsp \left.\... ...eft.\frac{g}{1-jz^{-1}}\right\vert _{z=-j} \eqsp \frac{g}{2}\,. \end{eqnarray*}

Thus,

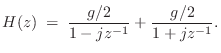
$\displaystyle H(z) \eqsp \frac{g/2}{1-jz^{-1}} + \frac{g/2}{1+jz^{-1}}. $

A more elaborate example of a partial fraction expansion into complex one-pole sections is given in §3.12.1.

Next Section:
PFE to Real, Second-Order Sections
Previous Section:
Example