Free Books    Introduction to Digital Filters  

Derivation of Group Delay as Modulation Delay

Suppose we write a narrowband signal centered at frequency $ \omega_c$ as

$\displaystyle x(n) = a_m(n) e^{j\omega_c n} \protect$ (8.6)

where $ \omega_c$ is defined as the carrier frequency (in radians per sample), and $ a_m(n)$ is some ``lowpass'' amplitude modulation signal. The modulation $ a_m$ can be complex-valued to represent either phase or amplitude modulation or both. By ``lowpass,'' we mean that the spectrum of $ a_m$ is concentrated near dc, i.e.,

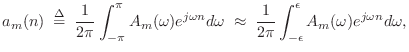
$\displaystyle a_m(n) \isdefs \frac{1}{2\pi} \int_{-\pi}^{\pi} A_m(\omega)e^{j\... ... \frac{1}{2\pi} \int_{-\epsilon}^{\epsilon} A_m(\omega)e^{j\omega n} d\omega, $

for some $ \left\vert\epsilon\right\vert\ll\pi$. The modulation bandwidth is thus bounded by $ 2\epsilon\ll\pi$.

Using the above frequency-domain expansion of $ a_m(n)$, $ x(n)$ can be written as

$\displaystyle x(n) \eqsp a_m(n) e^{j\omega_c n} \eqsp \left[\frac{1}{2\pi} \int_{-\epsilon}^{\epsilon} A_m(\omega)e^{j\omega n} d\omega\right] e^{j\omega_c n}, $

which we may view as a scaled superposition of sinusoidal components of the form

$\displaystyle x_\omega(n) \isdefs A_m(\omega)e^{j\omega n} e^{j\omega_c n} = A_m(\omega)e^{j(\omega+\omega_c) n} $

with $ \omega$ near 0. Let us now pass the frequency component $ x_\omega(n)$ through an LTI filter $ H(z)$ having frequency response

$\displaystyle H(e^{j\omega}) = G(\omega) e^{j\Theta(\omega)} $

to get

$\displaystyle y_\omega(n) = \left[G(\omega_c+\omega)A_m(\omega)\right] e^{j[(\omega_c +\omega) n + \Theta(\omega_c+\omega)]}. \protect$ (8.7)

Assuming the phase response $ \Theta(\omega)$ is approximately linear over the narrow frequency interval $ \omega\in[\omega_c-\epsilon,\omega_c+\epsilon]$, we can write

$\displaystyle \Theta(\omega_c+\omega)\;\approx\; \Theta(\omega_c) + \Theta^\prime(\omega_c)\omega \isdefs \Theta(\omega_c) - D(\omega_c)\omega, $

where $ D(\omega_c)$ is the filter group delay at $ \omega_c$. Making this substitution in Eq.$ \,$(7.7) gives

\begin{eqnarray*} y_\omega(n) &=& \left[G(\omega_c+\omega)A_m(\omega)\right] e^... ...\right] e^{j\omega[n-D(\omega_c)]} e^{j\omega_c[n-P(\omega_c)]}, \end{eqnarray*}

where we also used the definition of phase delay, $ P(\omega_c) = -\Theta(\omega_c)/\omega_c$, in the last step. In this expression we can already see that the carrier sinusoid is delayed by the phase delay, while the amplitude-envelope frequency-component is delayed by the group delay. Integrating over $ \omega$ to recombine the sinusoidal components (i.e., using a Fourier superposition integral for $ y$) gives

\begin{eqnarray*} y(n) &=& \frac{1}{2\pi}\int_{\omega} y_\omega(n) d\omega \\ &... ...)]}\\ &=& a^f[n-D(\omega_c)] \cdot e^{j\omega_c[n-P(\omega_c)]} \end{eqnarray*}

where $ a^f(n)$ denotes a zero-phase filtering of the amplitude envelope $ a(n)$ by $ G(\omega+\omega_c)$. We see that the amplitude modulation is delayed by $ D(\omega_c)$ while the carrier wave is delayed by $ P(\omega_c)$.

We have shown that, for narrowband signals expressed as in Eq.$ \,$(7.6) as a modulation envelope times a sinusoidal carrier, the carrier wave is delayed by the filter phase delay, while the modulation is delayed by the filter group delay, provided that the filter phase response is approximately linear over the narrowband frequency interval.

Next Section:
Two's Complement Wrap-Around
Previous Section:
Separating the Transfer Function Numerator and Denominator