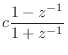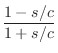Digitizing Analog Filters with the Bilinear Transformation

Free Books Introduction to Digital Filters

Digitizing Analog Filters with the
Bilinear Transformation

The desirable properties of many filter types (such as lowpass, highpass, and bandpass) are preserved very well by the $s\leftrightarrow z$ mapping called the bilinear transform.

Bilinear Transformation

The bilinear transform may be defined by

$\displaystyle s$	$\displaystyle =$	$\displaystyle c\frac{1-z^{-1}}{1+z^{-1}}\protect$	(I.9)
$\displaystyle z^{-1}$	$\displaystyle =$	$\displaystyle \frac{1-s/c}{1+s/c}\protect$	(I.10)

where

is an arbitrary positive constant that we may set to map one analog frequency precisely to one digital frequency. In the case of a lowpass or highpass filter,

is typically used to set the cut-off frequency to be identical in the analog and digital cases.

Frequency Warping

It is easy to check that the bilinear transform gives a one-to-one, order-preserving, conformal map [57] between the analog frequency axis $s=j\omega_a$ and the digital frequency axis $z=e^{j\omega_d T}$ , where is the sampling interval. Therefore, the amplitude response takes on exactly the same values over both axes, with the only defect being a frequency warping such that equal increments along the unit circle in the plane correspond to larger and larger bandwidths along the $j\omega$ axis in the plane [88]. Some kind of frequency warping is obviously unavoidable in any one-to-one map because the analog frequency axis is infinite while the digital frequency axis is finite. The relation between the analog and digital frequency axes may be derived immediately from Eq. $\,$ (I.9) as

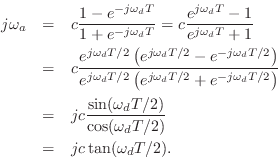
$\begin{eqnarray*} j\omega_a &=& c\frac{1-e^{-j\omega_d T}}{1+e^{-j\omega_d T}} =... ...sin(\omega_dT/2)}{\cos(\omega_dT/2)}\\ &=& jc\tan(\omega_dT/2). \end{eqnarray*}$

Given an analog cut-off frequency $\omega_a=\omega_c$ , to obtain the same cut-off frequency in the digital filter, we set

$\displaystyle c = \omega_c\cot(\omega_cT/2)$

Analog Prototype Filter

Since the digital cut-off frequency may be set to any value, irrespective of the analog cut-off frequency, it is convenient to set the analog cut-off frequency to $\omega_c = 1$ . In this case, the bilinear-transform constant is simply set to

$\displaystyle c = \cot(\omega_cT/2)$

when carrying out mapping Eq. $\,$ (I.9) to convert the analog prototype to a digital filter with cut-off at frequency $\omega_c$ .

Examples

Examples of using the bilinear transform to ``digitize'' analog filters may be found in §I.2 and [64,5,6,103,86]. Bilinear transform design is also inherent in the construction of wave digital filters [25,86].

Next Section:
Filter Design by Minimizing the L2 Equation-Error Norm
Previous Section:
Butterworth Lowpass Design