Example 2
For the filter
we obtain the output of residued (§J.6) shown in Fig.6.4. In contrast to residuez, residued delays the IIR part until after the FIR part. In contrast to this result, residuez returns r=[-24;16] and f=[10;2], corresponding to the PFE
| (7.22) |
in which the FIR and IIR parts have overlapping impulse responses.
See Sections J.5 and J.6 starting on page ![]() for
listings of residuez, residued and related
discussion.
for
listings of residuez, residued and related
discussion.
B=[2 6 6 2]; A=[1 -2 1]; [r,p,f,m] = residued(B,A) % r = % 8 % 16 % % p = % 1 % 1 % % f = % 2 10 % % m = % 1 % 2 |
Next Section:
Polynomial Multiplication in Matlab
Previous Section:
So What's Up with Repeated Poles?








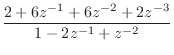
![$\displaystyle (2+10z^{-1}) + z^{-2}\left[\frac{8}{1-z^{-1}} + \frac{16}{(1-z^{-1})^2}\right]
\protect$](http://www.dsprelated.com/josimages_new/filters/img819.png)











