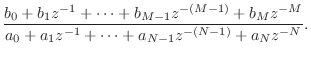Free Books
   Free Books    Introduction to Digital Filters  

Partial Fraction Expansion: residuez.m

Figure J.8 gives a listing of a matlab function for computing a ``left-justified'' partial fraction expansion (PFE) of an IIR digital filter $ H(z)=B(z)/A(z)$ as described in §6.8 (and below). This function, along with its ``right justified'' counterpart, residued, are included in the octave-forge matlab library for Octave.J.1

Figure J.8: Matlab/Octave function for computing the partial fraction expansion of an IIR digital filter.
  
function [r, p, f, m] = residuez(B, A, tol)
if nargin<3, tol=0.001; end
NUM = B(:)'; DEN = A(:)';
% Matlab's residue does not return m (implied by p):
[r,p,f,m]=residue(conj(fliplr(NUM)),conj(fliplr(DEN)),tol);
p = 1 ./ p;
r = r .* ((-p) .^m);
if f, f = conj(fliplr(f)); end

This code was written for Octave, but it also runs in Matlab if the 'm' outputs (pole multiplicity counts) are omitted (two places). The input arguments are compatible with the existing residuez function in the Matlab Signal Processing Toolbox.

Method

As can be seen from the code listing, this implementation of residuez simply calls residue, which was written to carry out the partial fraction expansions of $ s$-plane (continuous-time) transfer functions $ H(s)$:

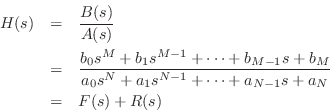
\begin{eqnarray*} H(s) &=& \frac{B(s)}{A(s)}\\ &=& \frac{b_0 s^M + b_1 s^{M-1}... ...s^N + a_1 s^{N-1} + \cdots + a_{N-1}s + a_N}\\ &=& F(s) + R(s) \end{eqnarray*}

where $ F(s)$ is the ``quotient'' and $ R(s)$ is the ``remainder'' in the PFE:

$\displaystyle F(s)$ $\displaystyle \isdef$ $\displaystyle f_0 s^L + f_1 s^{L-1} + \cdots + f_{L-1} s + f_L$  
$\displaystyle R(s)$ $\displaystyle \isdef$ $\displaystyle \frac{r_1}{(s-p_1)^m_1} + \cdots + \frac{r_N}{(s-p_N)^m_N} \protect$ (J.1)

where $ L=M-N$ is the order of the quotient polynomial in $ s$, and $ m_i$ is the multiplicity of the $ i$th pole. (When all poles are distinct, we have $ m_i=1$ for all $ i$.) For $ M<N$, we define $ F(s)=0$.

In the discrete-time case, we have the $ z$-plane transfer function

$\displaystyle H(z)$ $\displaystyle =$ $\displaystyle \frac{B(z)}{A(z)}$  
  $\displaystyle =$ $\displaystyle \frac{b_0 + b_1 z^{-1}+ \cdots + b_{M-1}z^{-(M-1)} + b_M z^{-M}} {a_0 + a_1 z^{-1}+ \cdots + a_{N-1}z^{-(N-1)} + a_N z^{-N}}. \protect$ (J.2)

For compatibility with Matlab's residuez, we need a PFE of the form $ H(z)=F(z)+R(z)$ such that

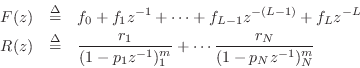
\begin{eqnarray*} F(z) &\isdef & f_0 + f_1 z^{-1}+ \cdots + f_{L-1} z^{-(L-1)} +... ...c{r_1}{(1-p_1z^{-1})^m_1} + \cdots \frac{r_N}{(1-p_Nz^{-1})^m_N} \end{eqnarray*}

where $ L=M-N$.

We see that the $ s$-plane case formally does what we desire if we treat $ z$-plane polynomials as polynomials in $ z^{-1}$ instead of $ z$. From Eq.$ \,$(J.2), we see that this requires reversing the coefficient-order of B and A in the call to residue. In the returned result, we obtain terms such as

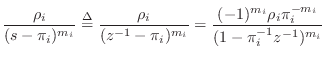
$\displaystyle \frac{\rho_i}{(s-\pi_i)^{m_i}} \isdef \frac{\rho_i}{(z^{-1}-\pi_i)^{m_i}} =\frac{(-1)^{m_i}\rho_i \pi_i^{-m_i}}{(1-\pi_i^{-1}z^{-1})^{m_i}} $

where the second form is simply the desired canonical form for $ z$-plane PFE terms. Thus, the $ i$th pole is

$\displaystyle p_i = \pi_i^{-1} $

and the $ i$th residue is

$\displaystyle r_i = \frac{\rho_i}{(-\pi_i)^{m_i}}. $

Finally, the returned quotient polynomial must be flipped for the same reason that the input polynomials needed to be flipped (to convert from left-to-right descending powers of $ z^{-1}$ [$ s$] in the returned result to ascending powers of $ z^{-1}$).

Example with Repeated Poles

The following Matlab code performs a partial fraction expansion of a filter having three pairs of repeated roots (one real and two complex):J.2

N = 1000;  % number of time samples to compute
A = [ 1 0 0 1 0 0 0.25];
B = [ 1 0 0 0 0 0 0];

% Compute "trusted" impulse response:
h_tdl = filter(B, A, [1 zeros(1, N-1)]);

% Compute partial fraction expansion (PFE):
[R,P,K] = residuez(B, A);

% PFE impulse response:
n = [0:N-1];
h_pfe = zeros(1,N);
for i = 1:size(R)
  % repeated roots are not detected exactly:
  if i>1 && abs(P(i)-P(i-1))<1E-7
    h_pfe = h_pfe + (R(i) * (n+1) .* P(i).^n);
    disp(sprintf('Pole %d is a repeat of pole %d',i,i-1));
    % if i>2 && abs(P(i)-P(i-2))<1E-7 ...
  else
    h_pfe = h_pfe + (R(i) * P(i).^n);
  end
end

err = abs(max(h_pfe-h_tdl)) % should be about 5E-8

Next Section:
Partial Fraction Expansion: residued.m
Previous Section:
Frequency Response Plots: plotfr.m