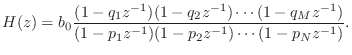DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Factored Form

By the fundamental theorem of algebra, every $ N$th order polynomial can be factored into a product of $ N$ first-order polynomials. Therefore, Eq.$ \,$(6.5) above can be written in factored form as

$\displaystyle H(z) = b_0\frac{(1-q_1z^{-1})(1-q_2z^{-1})\cdots(1-q_Mz^{-1})}{(1-p_1z^{-1})(1-p_2z^{-1})\cdots(1-p_Nz^{-1})}. \protect$ (7.6)

The numerator roots $ \{q_1,\ldots,q_M\}$ are called the zeros of the transfer function, and the denominator roots $ \{p_1, \ldots, p_N\}$ are called the poles of the filter. Poles and zeros are discussed further in Chapter 8.

Next Section:
Series and Parallel Transfer Functions
Previous Section:
Z Transform of Difference Equations