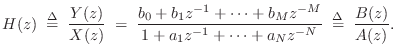Free Books
   Free Books    Introduction to Digital Filters  

Z Transform of Difference Equations

Since z transforming the convolution representation for digital filters was so fruitful, let's apply it now to the general difference equation, Eq.$ \,$(5.1). To do this requires two properties of the z transform, linearity (easy to show) and the shift theorem (derived in §6.3 above). Using these two properties, we can write down the z transform of any difference equation by inspection, as we now show. In §6.8.2, we'll show how to invert by inspection as well.

Repeating the general difference equation for LTI filters, we have (from Eq.$ \,$(5.1)) \begin{eqnarrayda} y(n) &=& b_0 x(n) &+& b_1 x(n - 1) + \cdots + b_M x(n - M)\\ & & &-& a_1 y(n - 1) - \cdots - a_N y(n - N).\\ \end{eqnarrayda}

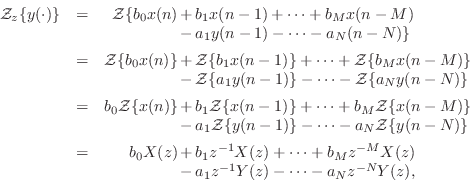Let's take the z transform of both sides, denoting the transform by $ {\cal Z}\{\}$. Because $ {\cal Z}\{\}$ is a linear operator, it may be distributed through the terms on the right-hand side as follows:7.3\begin{eqnarrayda} {\cal Z}_z\{y(\cdot)\} &=& {\cal Z}\{ b_0 x(n) &+& b_1 x(n ... ...-M} X(z)\\ & & &-& a_1 z^{-1}Y(z) - \cdots - a_N z^{-N} Y(z), \end{eqnarrayda} where we used the superposition and scaling properties of linearity given on page [*], followed by use of the shift theorem, in that order. The terms in $ Y(z)$ may be grouped together on the left-hand side to get

\begin{eqnarray*} \lefteqn{Y(z) + a_1 z^{-1}Y(z) + \cdots + a_N z^{-N} Y(z) = }\... ... \\ & & b_0 X(z) + b_1 z^{-1}X(z) + \cdots + b_M z^{-M} X(z). \end{eqnarray*}

Factoring out the common terms $ Y(z)$ and $ X(z)$ gives

$\displaystyle Y(z)\left[1 + a_1 z^{-1}+ \cdots + a_N z^{-N}\right] = X(z)\left[b_0 + b_1 z^{-1}+ \cdots + b_M z^{-M}\right]. $

Defining the polynomials

\begin{eqnarray*} A(z) &\isdef & 1 + a_1\,z^{-1} + \,\cdots\, + a_N\,z^{-N}\\ B(z) &\isdef & b_0 + b_1\,z^{-1}+\,\cdots\,+b_M\,z^{-M}, \end{eqnarray*}

the z transform of the difference equation yields

$\displaystyle A(z)\,Y(z) = B(z)\,X(z). $

Finally, solving for $ Y(z)/X(z)$, which is by definition the transfer function $ H(z)$, gives

$\displaystyle H(z) \isdefs \frac{Y(z)}{X(z)} \eqsp \frac{b_0 + b_1 z^{-1}+ \cdo... ...^{-M}}{1 + a_1 z^{-1}+ \cdots + a_N z^{-N}} \isdefs \frac{B(z)}{A(z)}. \protect$ (7.5)

Thus, taking the z transform of the general difference equation led to a new formula for the transfer function in terms of the difference equation coefficients. (Now the minus signs for the feedback coefficients in the difference equation Eq.$ \,$(5.1) are explained.)

Next Section:
Factored Form
Previous Section:
Z Transform of Convolution