Free Books    Introduction to Digital Filters  

Series and Parallel Transfer Functions

The transfer function conveniently captures the algebraic structure of a filtering operation with respect to series or parallel combination. Specifically, we have the following cases:

  1. Transfer functions of filters in series multiply together.
  2. Transfer functions of filters in parallel sum together.

Series Case

Figure 6.1: Series combination of transfer functions $ H_1(z)$ and $ H_2(z)$ to produce the combined transfer function $ H(z)=H_1(z)H_2(z)$.
\begin{figure}\input fig/series.pstex_t \end{figure}

Figure 6.1 illustrates the series connection of two filters $ H_1(z)=V(z)/X(z)$ and $ H_2(z)=Y(z)/V(z)$. The output $ v(n)$ from filter 1 is used as the input to filter 2. Therefore, the overall transfer function is

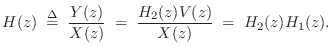
$\displaystyle H(z) \isdefs \frac{Y(z)}{X(z)} \eqsp \frac{H_2(z)V(z)}{X(z)} \eqsp H_2(z)H_1(z). $

In summary, if the output of filter $ H_1(z)$ is given as input to filter $ H_2(z)$ (a series combination), as shown in Fig.6.1, the overall transfer function is $ H(z)=H_1(z)H_2(z)$--transfer functions of filters connected in series multiply together.

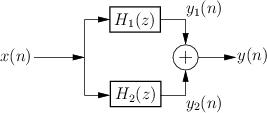
Parallel Case

Figure 6.2: Parallel combination of transfer functions $ H_1(z)$ and $ H_2(z)$, yielding $ H(z)=H_1(z)+H_2(z)$.
\begin{figure}\input fig/parallel.pstex_t \end{figure}

Figure 6.2 illustrates the parallel combination of two filters. The filters $ H_1(z)$ and $ H_2(z)$ are driven by the same input signal $ x(n)$, and their respective outputs $ y_1(n)$ and $ y_2(n)$ are summed. The transfer function of the parallel combination is therefore

$\displaystyle H(z) \isdefs \frac{Y(z)}{X(z)} \eqsp \frac{Y_1(z) + Y_2(z)}{X(z)} \eqsp \frac{Y_1(z)}{X(z)} + \frac{Y_2(z)}{X(z)} \isdefs H_1(z)+H_2(z). $

where we needed only linearity of the z transform to have that $ {\cal Z}\{y_1+y_2\} = {\cal Z}\{y_1\}+{\cal Z}\{y_2\}$.

Series Combination is Commutative

Since multiplication of complex numbers is commutative, we have

$\displaystyle H_1(z)H_2(z)=H_2(z)H_1(z), $

which implies that any ordering of filters in series results in the same overall transfer function. Note, however, that the numerical performance of the overall filter is usually affected by the ordering of filter stages in a series combination [103]. Chapter 9 further considers numerical performance of filter implementation structures.

By the convolution theorem for z transforms, commutativity of a product of transfer functions implies that convolution is commutative:

$\displaystyle h_1 \ast h_2 \;\leftrightarrow\; H_1\cdot H_2 \;=\; H_2\cdot H_1 \;\leftrightarrow\; h_2 \ast h_1 $

Next Section:
Partial Fraction Expansion
Previous Section:
Factored Form