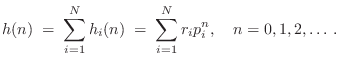DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Inverting the Z Transform

The partial fraction expansion (PFE) provides a simple means for inverting the z transform of rational transfer functions. The PFE provides a sum of first-order terms of the form

$\displaystyle H_i(z) \eqsp \frac{r_i}{1-p_iz^{-1}}. $

It is easily verified that such a term is the z transform of

$\displaystyle h_i(n) \eqsp r_i p_i^n, \quad n=0,1,2,\ldots\,. $

Thus, the inverse z transform of $ H(z)$ is simply

$\displaystyle h(n) \eqsp \sum_{i=1}^N h_i(n) \eqsp \sum_{i=1}^N r_i p_i^n, \quad n=0,1,2,\ldots\,. $

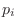
Thus, the impulse response of every strictly proper LTI filter (with distinct poles) can be interpreted as a linear combination of sampled complex exponentials. Recall that a uniformly sampled exponential is the same thing as a geometric sequence. Thus, $ h$ is a linear combination of $ N$ geometric sequences. The term ratio of the $ i$th geometric sequence is the $ i$th pole, $ p_i$, and the coefficient of the $ i$th sequence is the $ i$th residue, $ r_i$.

In the improper case, discussed in the next section, we additionally obtain an FIR part in the z transform to be inverted:

$\displaystyle F(z) \eqsp f_0 + f_1z^{-1}+ f_2z^{-2}+ \cdots + f_K z^{-K} \;\longleftrightarrow\; [f_0,f_1,\ldots,f_K,0,0,\ldots]. $

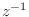
The FIR part (a finite-order polynomial in $ z^{-1}$) is also easily inverted by inspection.

The case of repeated poles is addressed in §6.8.5 below.

Next Section:
FIR Part of a PFE
Previous Section:
PFE to Real, Second-Order Sections