DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Laplace Analysis of Linear Systems

The differentiation theorem can be used to convert differential equations into algebraic equations, which are easier to solve. We will now show this by means of two examples.

Moving Mass

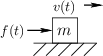
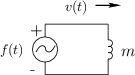
Figure D.1 depicts a free mass driven by an external force along an ideal frictionless surface in one dimension. Figure D.2 shows the electrical equivalent circuit for this scenario in which the external force is represented by a voltage source emitting $ f(t)$ volts, and the mass is modeled by an inductor having the value $ L=m$ Henrys.

Figure D.1: Physical diagram of an external force driving a mass along a frictionless surface.
\begin{figure}\input fig/forcemass.pstex_t \end{figure}

Figure: Electrical equivalent circuit of the force-driven mass in Fig.D.1.
\begin{figure}\input fig/forcemassec.pstex_t \end{figure}

From Newton's second law of motion ``$ f=ma$'', we have

$\displaystyle f(t) = m\,a(t) \isdef m\,{\dot v}(t) \isdef m\,{\ddot x}(t). $

Taking the unilateral Laplace transform and applying the differentiation theorem twice yields

\begin{eqnarray*} F(s) &=& m\,{\cal L}_s\{{\ddot x}\}\\ &=& m\left[\,s {\cal L... ...right\}\\ &=& m\left[s^2\,X(s) - s\,x(0) - {\dot x}(0)\right]. \end{eqnarray*}

Thus, given

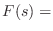  • $ F(s) = $ Laplace transform of the driving force $ f(t)$,
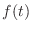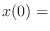  • $ x(0) = $ initial mass position, and
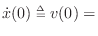  • $ {\dot x}(0)\isdeftext v(0) = $ initial mass velocity,
we can solve algebraically for $ X(s)$, the Laplace transform of the mass position for all $ t\ge 0$. This Laplace transform can then be inverted to obtain the mass position $ x(t)$ for all $ t\ge 0$. This is the general outline of how Laplace-transform analysis goes for all linear, time-invariant (LTI) systems. For nonlinear and/or time-varying systems, Laplace-transform analysis cannot, strictly speaking, be used at all.

If the applied external force $ f(t)$ is zero, then, by linearity of the Laplace transform, so is $ F(s)$, and we readily obtain

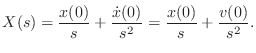
$\displaystyle X(s) = \frac{x(0)}{s} + \frac{{\dot x}(0)}{s^2} = \frac{x(0)}{s} + \frac{v(0)}{s^2}. $

Since $ 1/s$ is the Laplace transform of the Heaviside unit-step function

$\displaystyle u(t)\isdef \left\{\begin{array}{ll} 0, & t<0 \\ [5pt] 1, & t\ge 0 \\ \end{array}\right., $

we find that the position of the mass $ x(t)$ is given for all time by

$\displaystyle x(t) = x(0)\,u(t) + v(0)\,t\,u(t). $

Thus, for example, a nonzero initial position $ x(0)=x_0$ and zero initial velocity $ v(0)=0$ results in $ x(t)=x_0$ for all $ t\ge 0$; that is, the mass ``just sits there''.D.3 Similarly, any initial velocity $ v(0)$ is integrated with respect to time, meaning that the mass moves forever at the initial velocity.

To summarize, this simple example illustrated use the Laplace transform to solve for the motion of a simple physical system (an ideal mass) in response to initial conditions (no external driving forces). The system was described by a differential equation which was converted to an algebraic equation by the Laplace transform.

Mass-Spring Oscillator Analysis

Consider now the mass-spring oscillator depicted physically in Fig.D.3, and in equivalent-circuit form in Fig.D.4.

Figure D.3: An ideal mass $ m$ sliding on a frictionless surface, attached via an ideal spring $ k$ to a rigid wall. The spring is at rest when the mass is centered at $ x=0$.
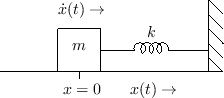\includegraphics{eps/massspringwall}

Figure D.4: Equivalent circuit for the mass-spring oscillator.
\begin{figure}\input fig/tankec.pstex_t \end{figure}

By Newton's second law of motion, the force $ f_m(t)$ applied to a mass equals its mass times its acceleration:

$\displaystyle f_m(t)=m{\ddot x}(t). $

By Hooke's law for ideal springs, the compression force $ f_k(t)$ applied to a spring is equal to the spring constant $ k$ times the displacement $ x(t)$:

$\displaystyle f_k(t)=kx(t) $

By Newton's third law of motion (``every action produces an equal and opposite reaction''), we have $ f_k = -f_m$. That is, the compression force $ f_k$ applied by the mass to the spring is equal and opposite to the accelerating force $ f_m$ exerted in the negative-$ x$ direction by the spring on the mass. In other words, the forces at the mass-spring contact-point sum to zero:

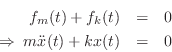
\begin{eqnarray*} f_m(t) + f_k(t) &=& 0\\ \Rightarrow\; m {\ddot x}(t) + k x(t) &=& 0 \end{eqnarray*}

We have thus derived a second-order differential equation governing the motion of the mass and spring. (Note that $ x(t)$ in Fig.D.3 is both the position of the mass and compression of the spring at time $ t$.)

Taking the Laplace transform of both sides of this differential equation gives

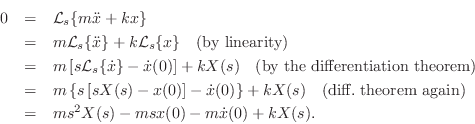
\begin{eqnarray*} 0 &=& {\cal L}_s\{m{\ddot x}+ k x\} \\ &=& m{\cal L}_s\{{\ddo... ...orem again)} \\ &=& ms^2 X(s) - msx(0) - m{\dot x}(0) + k X(s). \end{eqnarray*}

To simplify notation, denote the initial position and velocity by $ x(0)=x_0$ and $ {\dot x}(0)={\dot x}_0=v_0$, respectively. Solving for $ X(s)$ gives

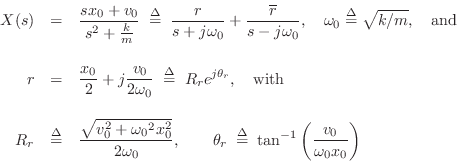
\begin{eqnarray*} X(s) &=& \frac{sx_0 + v_0}{s^2 + \frac{k}{m}} \;\isdef \; \fr... ...ta_r \;\isdef \; \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right) \end{eqnarray*}

denoting the modulus and angle of the pole residue $ r$, respectively. From §D.1, the inverse Laplace transform of $ 1/(s+a)$ is $ e^{-at}u(t)$, where $ u(t)$ is the Heaviside unit step function at time 0. Then by linearity, the solution for the motion of the mass is

\begin{eqnarray*} x(t) &=& re^{-j{\omega_0}t} + \overline{r}e^{j{\omega_0}t} = ... ...ga_0}t - \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right)\right]. \end{eqnarray*}

If the initial velocity is zero ($ v_0=0$), the above formula reduces to $ x(t) = x_0\cos({\omega_0}t)$ and the mass simply oscillates sinusoidally at frequency $ {\omega_0}= \sqrt{k/m}$, starting from its initial position $ x_0$. If instead the initial position is $ x_0=0$, we obtain

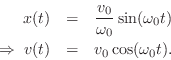
\begin{eqnarray*} x(t) &=& \frac{v_0}{{\omega_0}}\sin({\omega_0}t)\\ \;\Rightarrow\; v(t) &=& v_0\cos({\omega_0}t). \end{eqnarray*}

Next Section:
Example Analog Filter
Previous Section:
Laplace Transform Theorems