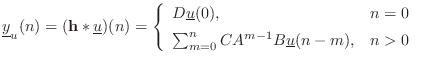Markov Parameters

Free Books Introduction to Digital Filters

The impulse response of a state-space model is easily found by direct calculation using Eq. $\,$ (G.1):

$\begin{eqnarray*} \mathbf{h}(0) &=& C {\underline{x}}(0) + D\,\underline{\delta}... ... B\\ [5pt] &\vdots&\\ \mathbf{h}(n) &=& C A^{n-1} B, \quad n>0 \end{eqnarray*}$

Note that we have assumed ${\underline{x}}(0)=0$ (zero initial state or zero initial conditions). The notation $\underline{\delta}(n)$ denotes a $q\times q$ matrix having $\delta (n)$ along the diagonal and zeros elsewhere.^G.2

The impulse response of the state-space model can be summarized as

$\displaystyle \fbox{$\displaystyle \mathbf{h}(n) = \left\{\begin{array}{ll} D, & n=0 \\ [5pt] CA^{n-1}B, & n>0 \\ \end{array} \right.$}$

(G.2)

The impulse response terms for $n\geq 0$ are known as the Markov parameters of the state-space model.

Note that each sample of the impulse response $\mathbf{h}(n)$ is a $p\times q$ matrix.^G.3 Therefore, it is not a possible output signal, except when . A better name might be ``impulse-matrix response''. In §G.4 below, we'll see that $\mathbf{h}(n)$ is the inverse z transform of the matrix transfer-function of the system.

Given an arbitrary input signal $\underline{u}(n)$ (and zero intial conditions ${\underline{x}}(0)=0$ ), the output signal is given by the convolution of the input signal with the impulse response:

$\displaystyle \underline{y}_u(n) = (\mathbf{h}\ast \underline{u})(n) = \left\{\... ... \sum_{m=0}^nCA^{m-1}B\underline{u}(n-m), & n>0 \\ \end{array} \right. \protect$