DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

One-Pole

Figure B.3: Signal flow graph for the general one-pole filter
$ y(n) = b_0 x(n) - a_1 y(n - 1).$
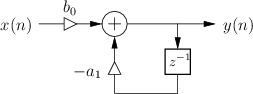
\begin{figure}\input fig/kfig2p20.pstex_t \end{figure}

Fig.B.3 gives the signal flow graph for the general one-pole filter. The road to the frequency response goes as follows:

Figure B.4: Family of frequency responses of the one-pole filter
$ y(n) = x(n) - a_1 y(n - 1)$
for various real values of $ a_1$. (a) Amplitude response. (b) Phase response.
\begin{figure}\input fig/kfig2p21.pstex_t \end{figure}

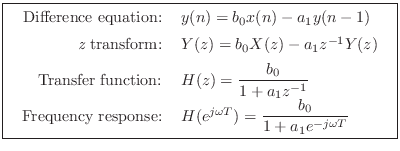
\fbox{ \begin{tabular}{rl} Difference equation: & $y(n) = b_0 x(n) - a_1 y(n-1)... ...$H(e^{j\omega T}) = \displaystyle\frac{b_0}{1+a_1e^{-j\omega T}}$ \end{tabular}}

The one-pole filter has a transfer function (hence frequency response) which is the reciprocal of that of a one-zero. The analysis is thus quite analogous. The frequency response in polar form is given by

\begin{eqnarray*} G(\omega) &=& \frac{\vert b_0\vert}{\sqrt{[1 + a_1 \cos(\omega... ... + a_1 \cos(\omega T)}\right], & b_0<0 \\ \end{array} \right.. \end{eqnarray*}

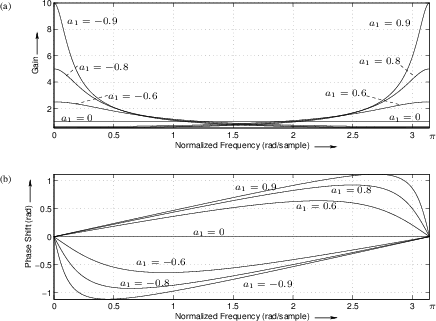
A plot of the frequency response in polar form for $ b_0 = 1$ and various values of $ a_1$ is given in Fig.B.4.

The filter has a pole at $ z = -a_1$, in the $ z$ plane (and a zero at $ z$ = 0). Notice that the one-pole exhibits either a lowpass or a highpass frequency response, like the one-zero. The lowpass character occurs when the pole is near the point $ z = 1$ (dc), which happens when $ a_1$ approaches $ -1$. Conversely, the highpass nature occurs when $ a_1$ is positive.

The one-pole filter section can achieve much more drastic differences between the gain at high frequencies and the gain at low frequencies than can the one-zero filter. This difference is achieved in the one-pole by gain boost in the passband rather than attenuation in the stopband; thus it is usually desirable when using a one-pole filter to set $ b_0$ to a small value, such as $ 1 - \left\vert a_1\right\vert$, so that the peak gain is 1 or so. When the peak gain is 1, the filter is unlikely to overflow.B.1

Finally, note that the one-pole filter is stable if and only if $ \left\vert a_1\right\vert < 1$.

Next Section:
Two-Pole
Previous Section:
One-Zero