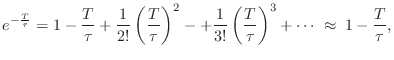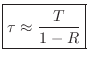Free Books    Introduction to Digital Filters  

Time Constant of One Pole

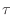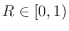A useful approximate formula giving the decay time-constant9.4 $ \tau$ (in seconds) in terms of a pole radius $ R\in[0,1)$ is

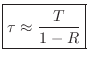$\displaystyle \zbox {\tau\approx \frac{T}{1-R}} \protect$ (9.8)

where $ T$ denotes the sampling interval in seconds, and we assume $ T\ll\tau$.

The exact relation between 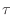$ \tau$ and $ R$ is obtained by sampling an exponential decay:

$\displaystyle e^{-t/\tau} \;\rightarrow\; e^{-nT/\tau} \;\isdef \; R^n $

Thus, setting $ n=1$ yields

$\displaystyle R = e^{-T/\tau}. $

Expanding the right-hand side in a Taylor series and neglecting terms higher than first order gives

$\displaystyle e^{-\frac{T}{\tau}} = 1 - \frac{T}{\tau} + \frac{1}{2!}\left(\fr... ...{1}{3!}\left(\frac{T}{\tau}\right)^3 + \cdots \;\approx\; 1 - \frac{T}{\tau}, $

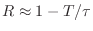
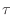
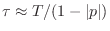
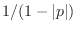
which derives $ R\approx 1-T/\tau$. Solving for $ \tau$ then gives Eq.$ \,$(8.8). From its derivation, we see that the approximation is valid for $ T\ll\tau$. Thus, as long as the impulse response of a pole $ p$ ``rings'' for many samples, the formula $ \tau\approx T/(1-\vert p\vert)$ should well estimate the time-constant of decay in seconds. The time-constant estimate in samples is of course $ 1/(1-\vert p\vert)$. 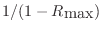For higher-order systems, the approximate decay time is $ 1/(1-R_{\mbox{max}})$, where $ R_{\mbox{max}}$ is the largest pole magnitude (closest to the unit circle) in the (stable) system.
Next Section:
Unstable Poles--Unit Circle Viewpoint
Previous Section:
Bandwidth of One Pole