The previous result can be extended toward bandlimited interpolation
of
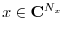 which includes all nonzero samples from an
arbitrary time-limited signal
which includes all nonzero samples from an
arbitrary time-limited signal
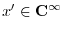 (i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
(i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
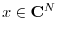 ) by
) by
- replacing the rectangular window
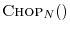 with a
smoother spectral window
with a
smoother spectral window 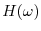 , and
, and
- using extra zero-padding in the time domain to convert the
cyclic convolution between
 and
and  into an
acyclic convolution between them (recall §7.2.4).
into an
acyclic convolution between them (recall §7.2.4).
The smoother spectral window
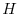
can be thought of as the
frequency response of the FIR
7.22 filter 
used as the
bandlimited interpolation kernel in the time domain. The number of
zeros needed in the zero-padding of

in the time domain is simply
length of

minus 1, and the number of zeros to be appended to

is the length of

minus 1. With this much
zero-padding, the
cyclic convolution of

and

implemented using
the
DFT becomes equivalent to acyclic convolution, as desired for the
time-limited signals

and

. Thus, if
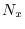
denotes the nonzero
length of

, then the nonzero length of

is

, and we require the DFT length to be

, where
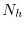
is the filter length. In operator
notation, we can express bandlimited
sampling-rate up-conversion by
the factor
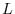
for time-limited signals
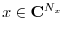
by
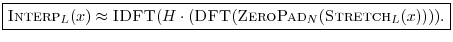 |
(7.8) |
The approximation symbol `
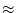
' approaches equality as the
spectral window
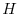
approaches
![$ \hbox{\sc Chop}_{N_x}([1,\dots,1])$](http://www.dsprelated.com/josimages_new/mdft/img1484.png)
(the
frequency response of the ideal
lowpass filter passing only the
original
spectrum 
), while at the same time allowing no time
aliasing (convolution remains acyclic in the time domain).
Equation (7.8) can provide the basis for a high-quality
sampling-rate conversion algorithm. Arbitrarily long signals can be
accommodated by breaking them into segments of length 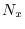 , applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter
, applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter  ``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when
``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when  is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter
is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter 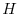 can
``window away'' more than the top
can
``window away'' more than the top 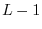 copies of
copies of  in
in 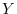 , thereby
preparing the time-domain signal for downsampling, say by
, thereby
preparing the time-domain signal for downsampling, say by
 :
:
where now the lowpass filter frequency response
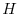
must be close to
zero for all
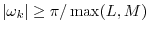
. While such a
sampling-rate conversion algorithm can be made more efficient by using
an
FFT in place of the DFT (see Appendix
A), it is not necessarily
the most efficient algorithm possible. This is because (1)
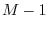
out
of

output samples from the IDFT need not be computed at all, and
(2)

has many zeros in it which do not need explicit
handling. For an introduction to time-domain sampling-rate
conversion (bandlimited interpolation) algorithms which take advantage
of points (1) and (2) in this paragraph, see,
e.g., Appendix
D and
[
72].
Next Section: Applying the Blackman WindowPrevious Section: Relation to Stretch Theorem
![]() which includes all nonzero samples from an
arbitrary time-limited signal
which includes all nonzero samples from an
arbitrary time-limited signal
![]() (i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
(i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
![]() ) by
) by
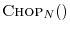 with a
smoother spectral window
with a
smoother spectral window 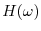 , and
, and
 and
and  into an
acyclic convolution between them (recall §7.2.4).
into an
acyclic convolution between them (recall §7.2.4).
![]() , applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter
, applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter ![]() ``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when
``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when ![]() is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter
is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter ![]() can
``window away'' more than the top
can
``window away'' more than the top ![]() copies of
copies of ![]() in
in ![]() , thereby
preparing the time-domain signal for downsampling, say by
, thereby
preparing the time-domain signal for downsampling, say by
![]() :
:



















