Relation to Stretch Theorem

It is instructive to interpret the periodic interpolation theorem in terms of the stretch theorem, $\hbox{\sc Stretch}_L(x) \;\longleftrightarrow\;\hbox{\sc Repeat}_L(X)$ . To do this, it is convenient to define a ``zero-centered rectangular window'' operator:

Definition: For any $X\in{\bf C}^N$ and any odd integer we define the length even rectangular windowing operation by

$\displaystyle \hbox{\sc Chop}_{M,k}(X) \isdef \left\{\begin{array}{ll} X(k), ... ...+1}{2} \leq \left\vert k\right\vert \leq \frac{N}{2}. \\ \end{array} \right.$

Thus, this ``zero-phase rectangular window,'' when applied to a spectrum

, sets the spectrum to zero everywhere outside a zero-centered interval of

samples. Note that $\hbox{\sc Chop}_M(X)$ is the ideal lowpass filtering operation in the frequency domain. The ``cut-off frequency'' is $\omega_c = 2\pi[(M-1)/2]/N$ radians per sample. For even

, we allow

to be ``passed'' by the window, but in our usage (below), this sample should always be zero anyway. With this notation defined we can efficiently restate periodic interpolation in terms of the $\hbox{\sc Stretch}()$ operator:

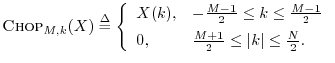
Theorem: When $x\in{\bf C}^N$ consists of one or more periods from a periodic signal $x^\prime\in {\bf C}^\infty$ ,

$\displaystyle \zbox {\hbox{\sc PerInterp}_L(x) = \hbox{\sc IDFT}(\hbox{\sc Chop}_N(\hbox{\sc DFT}(\hbox{\sc Stretch}_L(x)))).}$

In other words, ideal periodic interpolation of one period of

by the integer factor

may be carried out by first stretching

by the factor

(inserting

zeros between adjacent samples of

), taking the DFT, applying the ideal lowpass filter as an

-point rectangular window in the frequency domain, and performing the inverse DFT.

Proof: First, recall that $\hbox{\sc Stretch}_L(x)\leftrightarrow \hbox{\sc Repeat}_L(X)$ . That is, stretching a signal by the factor gives a new signal $y=\hbox{\sc Stretch}_L(x)$ which has a spectrum consisting of copies of repeated around the unit circle. The ``baseband copy'' of in can be defined as the -sample sequence centered about frequency zero. Therefore, we can use an ``ideal filter'' to ``pass'' the baseband spectral copy and zero out all others, thereby converting $\hbox{\sc Repeat}_L(X)$ to $\hbox{\sc ZeroPad}_{LN}(X)$ . I.e.,