Correlation
The correlation operator for two signals ![]() and
and ![]() in
in ![]() is defined as
is defined as
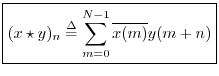
We may interpret the correlation operator as
Next Section:
Stretch Operator
Previous Section:
Convolution
The correlation operator for two signals ![]() and
and ![]() in
in ![]() is defined as
is defined as
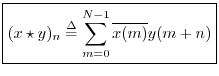
We may interpret the correlation operator as