DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

The Discrete Fourier Transform (DFT)

Given a signal $ x(\cdot)\in{\bf C}^N$, its DFT is defined by6.3

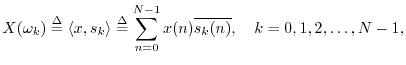
$\displaystyle X(\omega_k) \isdef \left<x,s_k\right> \isdef \sum_{n=0}^{N-1}x(n) \overline{s_k(n)}, \quad k=0,1,2,\ldots,N-1, $

where

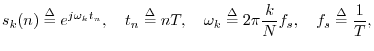
$\displaystyle s_k(n)\isdef e^{j\omega_k t_n}, \quad t_n\isdef nT, \quad \omega_k\isdef 2\pi\frac{k}{N}f_s, \quad f_s\isdef \frac{1}{T}, $

or, as it is most often written,

$\displaystyle \zbox {X(\omega_k) \isdef \sum_{n=0}^{N-1}x(n) e^{-j\frac{2\pi k n}{N}}, \quad k=0,1,2,\ldots,N-1.} $

We may also refer to $ X$ as the spectrum of $ x$, and $ X(\omega_k)$ is the $ k$th sample of the spectrum at frequency $ \omega_k$. Thus, the $ k$th sample $ X(\omega_k)$ of the spectrum of $ x$ is defined as the inner product of $ x$ with the $ k$th DFT sinusoid $ s_k$. This definition is $ N$ times the coefficient of projection of $ x$ onto $ s_k$, i.e.,

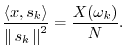
$\displaystyle \frac{\left<x,s_k\right>}{\left\Vert\,s_k\,\right\Vert^2} = \frac{X(\omega_k)}{N}. $

The projection of $ x$ onto $ s_k$ is

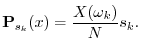
$\displaystyle {\bf P}_{s_k}(x) = \frac{X(\omega_k)}{N} s_k. $

Since the $ \{s_k\}$ are orthogonal and span $ {\bf C}^N$, using the main result of the preceding chapter, we have that the inverse DFT is given by the sum of the projections

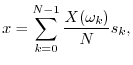
$\displaystyle x = \sum_{k=0}^{N-1}\frac{X(\omega_k)}{N} s_k, $

or, as we normally write,

$\displaystyle \zbox {x(n) = \frac{1}{N} \sum_{k=0}^{N-1}X(\omega_k) e^{j\frac{2\pi k n}{N}}, \quad n=0,1,\ldots,N-1.} \protect$ (6.1)

In summary, the DFT is proportional to the set of coefficients of projection onto the sinusoidal basis set, and the inverse DFT is the reconstruction of the original signal as a superposition of its sinusoidal projections. This basic ``architecture'' extends to all linear orthogonal transforms, including wavelets, Fourier transforms, Fourier series, the discrete-time Fourier transform (DTFT), and certain short-time Fourier transforms (STFT). See Appendix B for some of these.

We have defined the DFT from a geometric signal theory point of view, building on the preceding chapter. See §7.1.1 for notation and terminology associated with the DFT.

Next Section:
Frequencies in the ``Cracks''
Previous Section:
An Orthonormal Sinusoidal Set