An Orthonormal Sinusoidal Set
We can normalize the DFT sinusoids to obtain an orthonormal set:
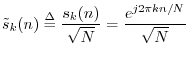
![$\displaystyle \left<\tilde{s}_k,\tilde{s}_l\right> = \left\{\begin{array}{ll}
1, & k=l \\ [5pt]
0, & k\neq l. \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1034.png)
Next Section:
The Discrete Fourier Transform (DFT)
Previous Section:
Norm of the DFT Sinusoids
We can normalize the DFT sinusoids to obtain an orthonormal set:
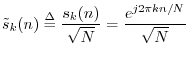
![$\displaystyle \left<\tilde{s}_k,\tilde{s}_l\right> = \left\{\begin{array}{ll}
1, & k=l \\ [5pt]
0, & k\neq l. \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1034.png)