Free Books
   Free Books    Mathematics of the DFT  

Normalized DFT Power Theorem

Note that the power theorem would be more elegant if the DFT were defined as the coefficient of projection onto the normalized DFT sinusoids

$\displaystyle \tilde{s}_k(n) \isdef \frac{s_k(n)}{\sqrt{N}}. $

That is, for the normalized DFT (§6.10), the power theorem becomes simply

$\displaystyle \left<x,y\right> = \langle \tilde{X},\tilde{Y}\rangle$   (Normalized DFT case)$\displaystyle . \protect$

We see that the power theorem expresses the invariance of the inner product between two signals in the time and frequency domains. If we think of the inner product geometrically, as in Chapter 5, then this result is expected, because $ x$ and $ \tilde{X}$ are merely coordinates of the same geometric object (a signal) relative to two different sets of basis signals (the shifted impulses and the normalized DFT sinusoids).

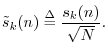
Next Section:
Illustration of the Downsampling/Aliasing Theorem in Matlab
Previous Section:
Application of the Shift Theorem to FFT Windows