DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Normalized DFT

A more ``theoretically clean'' DFT is obtained by projecting onto the normalized DFT sinusoids (§6.5)

$\displaystyle \tilde{s}_k(n) \isdef \frac{e^{j2\pi k n/N}}{\sqrt{N}}. $

In this case, the normalized DFT (NDFT) of $ x$ is

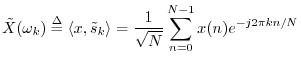
$\displaystyle \tilde{X}(\omega_k) \isdef \left<x,\tilde{s}_k\right> = \frac{1}{\sqrt{N}}\sum_{n=0}^{N-1}x(n) e^{-j2\pi k n/N} $

which is also precisely the coefficient of projection of $ x$ onto $ \tilde{s}_k$. The inverse normalized DFT is then more simply

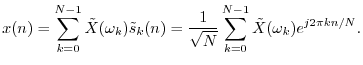
$\displaystyle x(n) = \sum_{k=0}^{N-1}\tilde{X}(\omega_k) \tilde{s}_k(n) = \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\tilde{X}(\omega_k)e^{j2\pi k n/N}. $

While this definition is much cleaner from a ``geometric signal theory'' point of view, it is rarely used in practice since it requires slightly more computation than the typical definition. However, note that the only difference between the forward and inverse transforms in this case is the sign of the exponent in the kernel. Advantages of the NDFT over the DFT in fixed-point implementations (Appendix G) are discussed in Appendix A.

It can be said that only the NDFT provides a proper change of coordinates from the time-domain (shifted impulse basis signals) to the frequency-domain (DFT sinusoid basis signals). That is, only the NDFT is a pure rotation in $ {\bf C}^N$, preserving both orthogonality and the unit-norm property of the basis functions. The DFT, in contrast, preserves orthogonality, but the norms of the basis functions grow to $ \sqrt{N}$. Therefore, in the present context, the DFT coefficients can be considered ``denormalized'' frequency-domain coordinates.

Next Section:
The Length 2 DFT
Previous Section:
Fourier Series Special Case