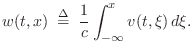DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Converting Any String State to Traveling Slope-Wave Components

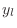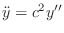We verified in §C.3.1 above that traveling-wave components $ y_r$ and $ y_l$ in Eq.$ \,$(C.14) satisfy the ideal string wave equation $ {\ddot y}= c^2y''$. By definition, the physical string displacement is given by the sum of the traveling-wave components, or

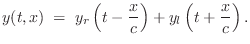$\displaystyle y(t,x) \eqsp y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right). \protect$ (C.15)

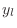
Thus, given any pair of traveling waves $ y_r$ and $ y_l$, we can compute a corresponding string displacement $ y$. This leads to the question whether any initial string state can be converted to a pair of equivalent traveling-wave components. If so, then d'Alembert's traveling-wave solution is complete, and all solutions to the ideal string wave equation can be expressed in terms of traveling waves.

The state of an ideal string at time $ t$ is classically specified by its displacement $ y(t,x)$ and velocity

$\displaystyle v(t,x)\isdefs {\dot y}(t,x)\isdefs \frac{\partial}{\partial t} y(t,x) $

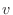
for all $ x$ [317]. Equation (C.15) gives us $ y$ as a simple sum of the traveling-wave components, and now we need a formula for $ v$ in terms of them as well. It will be derived in §C.7.3 (see Equations (C.44-C.46)) that we can write

$\displaystyle v(t,x) \eqsp -cy_r^\prime\left(t-\frac{x}{c}\right) + cy_l^\prime\left(t+\frac{x}{c}\right). $

where $ y'$ denotes the partial derivative with respect to $ x$ as usual. We have

$\displaystyle \left[\begin{array}{c} y(t,x) \\ [2pt] v(t,x) \end{array}\right] ... ...ght] \left[\begin{array}{c} y_r(t-x/c) \\ [2pt] y_l(t+x/c) \end{array}\right]. $

Inverting the two-by-two differential operator matrix yields left- and right-going slope waves as a function of an arbitrary initial slope and velocity:

$\displaystyle \left[\begin{array}{c} y'^{+} \\ [2pt] y'^{-} \end{array}\right] ... ...eft[\begin{array}{c} y'-\frac{v}{c} \\ [2pt] y'+\frac{v}{c} \end{array}\right] $

Integrating both sides with respect to $ x$, and choosing the constant of integration to give the correct constant component of $ y$, we obtain the displacement-wave components

$\displaystyle \left[\begin{array}{c} y^{+} \\ [2pt] y^{-} \end{array}\right] \eqsp \frac{1}{2}\left[\begin{array}{c} y-w \\ [2pt] y+w \end{array}\right] $

where

$\displaystyle w(t,x) \isdefs \frac{1}{c}\int_{-\infty}^x v(t,\xi)\,d\xi. $

Notice that if the initial velocity is zero, each of the initial traveling displacement waves is simply half the initial displacement, as expected. On the other hand, if the initial displacement is zero and there is a uniform initial velocity (the whole string is moving), the initial displacement-wave components are unbounded as the string length goes to infinity. Related discussion appears in Appendix E.

It will be seen in §C.7.4 that state conversion between physical variables and traveling-wave components is simpler when force and velocity are chosen as the physical state variables (as opposed to displacement and velocity used here).

Next Section:
Digital Waveguide Model
Previous Section:
D'Alembert Derived