Free Books    Physical Audio Signal Processing  

Comb Filters

Comb filters are basic building blocks for digital audio effects. The acoustic echo simulation in Fig.2.9 is one instance of a comb filter. This section presents the two basic comb-filter types, feedforward and feedback, and gives a frequency-response analysis.

Feedforward Comb Filters

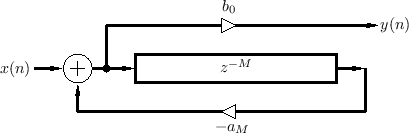
The feedforward comb filter is shown in Fig.2.23. The direct signal ``feeds forward'' around the delay line. The output is a linear combination of the direct and delayed signal.

Figure 2.23: The feedforward comb filter.
\includegraphics{eps/ffcf}

The ``difference equation'' [449] for the feedforward comb filter is

$\displaystyle y(n) = b_0 x(n) + b_M x(n-M). \protect$ (3.2)

We see that the feedforward comb filter is a particular type of FIR filter. It is also a special case of a TDL.

Note that the feedforward comb filter can implement the echo simulator of Fig.2.9 by setting $ b_0=1$ and $ b_M=g$. Thus, it is is a computational physical model of a single discrete echo. This is one of the simplest examples of acoustic modeling using signal processing elements. The feedforward comb filter models the superposition of a ``direct signal'' $ b_0 x(n)$ plus an attenuated, delayed signal $ b_M x(n-M)$, where the attenuation (by $ \vert b_M\vert<1$) is due to ``air absorption'' and/or spherical spreading losses, and the delay is due to acoustic propagation over the distance $ cMT$ meters, where $ T$ is the sampling period in seconds, and $ c$ is sound speed. In cases where the simulated propagation delay needs to be more accurate than the nearest integer number of samples $ M$, some kind of delay-line interpolation needs to be used (the subject of §4.1). Similarly, when air absorption needs to be simulated more accurately, the constant attenuation factor $ b_M$ can be replaced by a linear, time-invariant filter $ G(z)$ giving a different attenuation at every frequency. Due to the physics of air absorption, $ G(z)$ is generally lowpass in character [349, p. 560], [47,318].

Feedback Comb Filters

The feedback comb filter uses feedback instead of a feedforward signal, as shown in Fig.2.24 (drawn in ``direct form 2'' [449]).

Figure 2.24: The feedback comb filter.
\includegraphics{eps/fbcf}

A difference equation describing the feedback comb filter can be written in ``direct form 1'' [449] as3.9

$\displaystyle y(n) = b_0 x(n) - a_M y(n-M). $

The feedback comb filter is a special case of an Infinite Impulse Response (IIR) (``recursive'') digital filter, since there is feedback from the delayed output to the input [449]. The feedback comb filter can be regarded as a computational physical model of a series of echoes, exponentially decaying and uniformly spaced in time. For example, the special case

$\displaystyle y(n) = x(n) + g\, y(n-M) $

is a computational model of an ideal plane wave bouncing back and forth between two parallel walls; in such a model, $ g$ represents the total round-trip attenuation (two wall-to-wall traversals, including two reflections).

For stability, the feedback coefficient $ a_M$ must be less than $ 1$ in magnitude, i.e., $ \left\vert a_M\right\vert<1$. Otherwise, if $ \left\vert a_M\right\vert>1$, each echo will be louder than the previous echo, producing a never-ending, growing series of echoes.

Sometimes the output signal is taken from the end of the delay line instead of the beginning, in which case the difference equation becomes

$\displaystyle y(n) = b_M x(n-M) - a_M y(n-M) . $

This choice of output merely delays the output signal by $ M$ samples.

Feedforward Comb Filter Amplitude Response

Comb filters get their name from the ``comb-like'' appearance of their amplitude response (gain versus frequency), as shown in Figures 2.25, 2.26, and 2.27. For a review of frequency-domain analysis of digital filters, see, e.g., [449].

Figure: Amplitude responses of the feed forward comb-filter $ H(z) = x(n) + g x(n-M)$ (diagrammed in Fig.2.23) with $ M=5$ and $ g=0.1$, $ 0.5$, and $ 0.9$. a) Linear amplitude scale. b) Decibel scale. The frequency axis goes from 0 to the sampling rate (instead of only half the sampling rate, which is more typical for real filters) in order to display the fact that the number of notches is exactly $ M=5$ (as opposed to ``$ 2.5$'').
\includegraphics[width=\twidth ]{eps/ffcfar}

The transfer function of the feedforward comb filter Eq.$ \,$(2.2) is

$\displaystyle H(z) = b_0+b_M\,z^{-M},$ (3.3)

so that the amplitude response (gain versus frequency) is

$\displaystyle G(\omega) \isdef \left\vert H(e^{j\omega})\right\vert = \left\vert b_0 + b_M e^{-j\omega M}\right\vert, \quad -\pi \leq \omega \leq \pi. \protect$ (3.4)

This is plotted in Fig.2.25 for $ M=5$, $ b_0=1$, and $ b_M=0.1$, $ 0.5$, and $ 0.9$. When $ b_0=b_M=1$, we get the simplified result

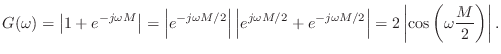
$\displaystyle G(\omega) = \left\vert 1 + e^{-j\omega M}\right\vert = \left\vert... ...ga M/2}\right\vert = 2\left\vert\cos\left(\omega\frac{M}{2}\right)\right\vert. $

In this case, we obtain $ M$ nulls, which are points (frequencies) of zero gain in the amplitude response. Note that in flangers, these nulls are moved slowly over time by modulating the delay length $ M$. Doing this smoothly requires interpolated delay lines (see Chapter 4 and Chapter 5).

Feedback Comb Filter Amplitude Response

Figure 2.26 shows a family of feedback-comb-filter amplitude responses, obtained using a selection of feedback coefficients.

Figure: Amplitude response of the feedback comb-filter $ H(z) = 1/(1-g z^{-M})$ (Fig.2.24 with $ b_0=1$ and $ -a_M=g$) with $ M=5$ and $ g=0.1$, $ 0.5$, and $ 0.9$. a) Linear amplitude scale. b) Decibel scale.
\includegraphics[width=\twidth ]{eps/fbcfar}

Figure 2.27 shows a similar family obtained using negated feedback coefficients; the opposite sign of the feedback exchanges the peaks and valleys in the amplitude response.

Figure: Amplitude response of the phase-inverted feedback comb-filter, i.e., as in Fig.2.26 with negated $ g=-0.1$, $ -0.5$, and $ -0.9$. a) Linear amplitude scale. b) Decibel scale.
\includegraphics[width=\twidth ]{eps/fbcfiar}

As introduced in §2.6.2 above, a class of feedback comb filters can be defined as any difference equation of the form

$\displaystyle y(n) = x(n) + g\,y(n-M). $

Taking the z transform of both sides and solving for $ H(z)\isdef Y(z)/X(z)$, the transfer function of the feedback comb filter is found to be

$\displaystyle H(z) = \frac{1}{1-g\,z^{-M}}, \protect$ (3.5)

so that the amplitude response is

$\displaystyle G(\omega) \isdef \left\vert H(e^{j\omega})\right\vert = \frac{1}{\left\vert 1 - g e^{-j\omega M}\right\vert}, \quad -\pi \leq \omega \leq \pi . $

This is plotted in Fig.2.26 for $ M=5$ and $ g=0.1$, $ 0.5$, and $ 0.9$. Figure 2.27 shows the same case but with the feedback sign-inverted.

For $ g=1$, the feedback-comb amplitude response reduces to

$\displaystyle G(\omega) = \frac{1}{2\left\vert\sin(\omega M/2)\right\vert}, $

and for $ g=-1$ to

$\displaystyle G(\omega) = \frac{1}{2\left\vert\cos(\omega M/2)\right\vert}, $

which exactly inverts the amplitude response of the feedforward comb filter with gain $ g=1$ (Eq.$ \,$(2.4)).

Note that $ g>0$ produces resonant peaks at

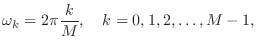
$\displaystyle \omega_k = 2\pi\frac{k}{M}, \quad k=0,1,2,\dots,M-1, $

while for $ g<0$, the peaks occur midway between these values.

Filtered-Feedback Comb Filters

The filtered-feedback comb filter (FFBCF) uses filtered feedback instead of just a feedback gain.

Denoting the feedback-filter transfer function by $ H_l(z)$, the transfer function of the filtered-feedback comb filter can be written as

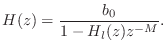
$\displaystyle H(z) = \frac{b_0}{1 - H_l(z)z^{-M}}. $

Note that when $ H_l(z)$ is a causal filter, the FFBCF can be considered mathematically a special case of the general allpole transfer function in which the first $ M-1$ denominator coefficients are constrained to be zero:

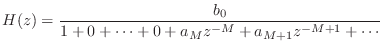
$\displaystyle H(z) = \frac{b_0}{1 + 0 + \cdots + 0 + a_M z^{-M} + a_{M+1} z^{-{M+1}} + \cdots} $

It is this ``sparseness'' of the filter coefficients that makes the FFBCF more computationally efficient than other, more general-purpose, IIR filter structures.

In §2.6.2 above, we mentioned the physical interpretation of a feedback-comb-filter as simulating a plane-wave bouncing back and forth between two walls. Inserting a lowpass filter in the feedback loop further simulates frequency dependent losses incurred during a propagation round-trip, as naturally occurs in real rooms.

The main physical sources of plane-wave attenuation are air absorption (§B.7.15) and the coefficient of absorption at each wall [349]. Additional ``losses'' for plane waves in real rooms occur due to scattering. (The plane wave hits something other than a wall and reflects off in many different directions.) A particular scatterer used in concert halls is textured wall surfaces. In ray-tracing simulations, reflections from such walls are typically modeled as having a specular and diffuse component. Generally speaking, wavelengths that are large compared with the ``grain size'' of the wall texture reflect specularly (with some attenuation due to any wall motion), while wavelengths on the order of or smaller than the texture grain size are scattered in various directions, contributing to the diffuse component of reflection.

The filtered-feedback comb filter has many applications in computer music. It was evidently first suggested for artificial reverberation by Schroeder [412, p. 223], and first implemented by Moorer [314]. (Reverberation applications are discussed further in §3.6.) In the physical interpretation [428,207] of the Karplus-Strong algorithm [236,233], the FFBCF can be regarded as a transfer-function physical-model of a vibrating string. In digital waveguide modeling of string and wind instruments, FFBCFs are typically derived routinely as a computationally optimized equivalent forms based on some initial waveguide model developed in terms of bidirectional delay-lines (``digital waveguides'') (see §6.10.1 for an example).

For stability, the amplitude-response of the feedback-filter $ H_l(z)$ must be less than $ 1$ in magnitude at all frequencies, i.e., $ \left\vert H_l(e^{j\omega T})\right\vert<1,\,\forall\omega T\in[-\pi,\pi)$.

Equivalence of Parallel Combs to TDLs

It is easy to show that the TDL of Fig.2.19 is equivalent to a parallel combination of three feedforward comb filters, each as in Fig.2.23. To see this, we simply add the three comb-filter transfer functions of Eq.$ \,$(2.3) and equate coefficients:

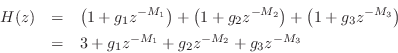
\begin{eqnarray*} H(z) &=& \left(1+g_1 z^{-M_1}\right) + \left(1+g_2 z^{-M_2}\... ...\right) \\ &=& 3 + g_1 z^{-M_1} + g_2 z^{-M_2} + g_3 z^{-M_3} \end{eqnarray*}

which implies

$\displaystyle b_0 = 3,\; b_{M_1} = g_1,\; b_{M_2} = g_2,\; b_{M_3} = g_3 . $

We see that parallel comb filters require more delay memory ( $ M_1+M_2+M_3$ elements) than the corresponding TDL, which only requires $ \max(M_1,M_2,M_3)$ elements.

Equivalence of Series Combs to TDLs

It is also straightforward to show that a series combination of feedforward comb filters produces a sparsely tapped delay line as well. Considering the case of two sections, we have

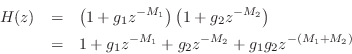
\begin{eqnarray*} H(z) &=& \left(1+g_1 z^{-M_1}\right) \left(1+g_2 z^{-M_2}\right)\\ &=& 1 + g_1 z^{-M_1} + g_2 z^{-M_2} + g_1 g_2 z^{-(M_1+M_2)} \end{eqnarray*}

which yields

$\displaystyle b_0 = 1,\; b_{M_1} = g_1,\; b_{M_2} = g_2,\; M_3=M_1+M_2,\;b_{M_3}=g_1 g_2. $

Thus, the TDL of Fig.2.19 is equivalent also to the series combination of two feedforward comb filters. Note that the same TDL structure results irrespective of the series ordering of the component comb filters.

Time Varying Comb Filters

Comb filters can be changed slowly over time to produce the following digital audio ``effects'', among others:

Since all of these effects involve modulating delay length over time, and since time-varying delay lines typically require interpolation, these applications will be discussed after Chapter 5 which covers variable delay lines. For now, we will pursue what can be accomplished using fixed (time-invariant) delay lines. Perhaps the most important application is artificial reverberation, addressed in Chapter 3.

Next Section:
Feedback Delay Networks (FDN)
Previous Section:
Tapped Delay Line (TDL)