DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Delay Loop Expansion

When a subset of the resonating modes are nearly harmonically tuned, it can be much more computationally efficient to use a filtered delay loop (see §2.6.5) to generate an entire quasi-harmonic series of modes rather than using a biquad for each modal peak [439]. In this case, the resonator model becomes

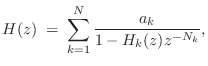
$\displaystyle H(z) \eqsp \sum_{k=1}^N \frac{a_k}{1 - H_k(z) z^{-N_k}}, $

where $ N_k$ is the length of the delay line in the $ k$th comb filter, and $ H_k(z)$ is a low-order filter which can be used to adjust finely the amplitudes and frequencies of the resonances of the $ k$th comb filter [428]. Recall (Chapter 6) that a single filtered delay loop efficiently models a distributed 1D propagation medium such as a vibrating string or acoustic tube. More abstractly, a superposition of such quasi-harmonic mode series can provide a computationally efficient psychoacoustic equivalent approximation to arbitrary collections of modes in the range of human hearing.

Note that when $ H_k(z)$ is close to $ -1$ instead of $ +1$, primarily only odd harmonic resonances are produced, as has been used in modeling the clarinet [431].

Next Section:
Measured Amplitude Response
Previous Section:
State Space Approach to Modal Expansions