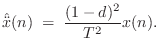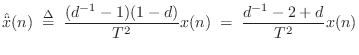Free Books    Physical Audio Signal Processing  

Delay Operator Notation

It is convenient to think of the FDA in terms of time-domain difference operators using a delay operator notation. The delay operator $ d$ is defined by

$\displaystyle d^k x(n) \eqsp x(n-k). $

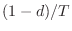
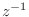
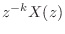
Thus, the first-order difference (derivative approximation) is represented in the time domain by $ (1-d)/T$. We can think of $ d$ as $ z^{-1}$ since, by the shift theorem for $ z$ transforms, $ z^{-k} X(z)$ is the $ z$ transform of $ x$ delayed (right shifted) by $ k$ samples.

The obvious definition for the second derivative is

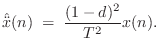$\displaystyle {\hat{\ddot x}}(n) \eqsp \frac{(1-d)^2}{T^2} x(n).$ (8.4)

However, a better definition is the centered finite difference

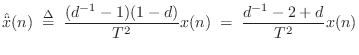$\displaystyle {\hat{\ddot x}}(n) \isdefs \frac{(d^{-1}-1)(1-d)}{T^2} x(n) \eqsp \frac{d^{-1}-2+d}{T^2}x(n) \protect$ (8.5)

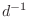
where $ d^{-1}$ denotes a unit-sample advance. This definition is preferable as long as one sample of look-ahead is available, since it avoids an operator delay of one sample. Equation (7.5) is a zero phase filter, meaning it has no delay at any frequency, while (7.4) is a linear phase filter having a delay of $ 1$ sample at all frequencies.

Next Section:
Finite Difference Approximation vs. Bilinear Transform
Previous Section:
FDA in the Frequency Domain