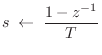FDA in the Frequency Domain
Viewing Eq.![]() (7.2) in the frequency domain, the ideal
differentiator transfer-function is
(7.2) in the frequency domain, the ideal
differentiator transfer-function is ![]() , which can be viewed as
the Laplace transform of the operator
, which can be viewed as
the Laplace transform of the operator ![]() (left-hand side of
Eq.
(left-hand side of
Eq.![]() (7.2)). Moving to the right-hand side, the z transform of the
first-order difference operator is
(7.2)). Moving to the right-hand side, the z transform of the
first-order difference operator is
![]() . Thus, in the
frequency domain, the finite-difference approximation may be performed
by making the substitution
. Thus, in the
frequency domain, the finite-difference approximation may be performed
by making the substitution
in any continuous-time transfer function (Laplace transform of an integro-differential operator) to obtain a discrete-time transfer function (z transform of a finite-difference operator).
The inverse of substitution Eq.![]() (7.3) is
(7.3) is
As discussed in §8.3.1, the FDA is a special case of the
matched ![]() transformation applied to the point
transformation applied to the point ![]() .
.
Note that the FDA does not alias, since the conformal mapping
![]() is one to one. However, it does warp the poles and zeros in a
way which may not be desirable, as discussed further on p.
is one to one. However, it does warp the poles and zeros in a
way which may not be desirable, as discussed further on p. ![]() below.
below.
Next Section:
Delay Operator Notation
Previous Section:
Practical Advice