The Leslie
The Leslie, named after its inventor, Don Leslie,6.9 is a popular audio processor used with electronic organs and other instruments [59,189]. It employs a rotating horn and rotating speaker port to ``choralize'' the sound. Since the horn rotates within a cabinet, the listener hears multiple reflections at different Doppler shifts, giving a kind of chorus effect. Additionally, the Leslie amplifier distorts at high volumes, producing a pleasing ``growl'' highly prized by keyboard players. At the time of this writing, there is a nice Leslie Wikipedia page, including a stereo sound-example link under the first picture (that is best heard in headphones). Papers on computational audio models of the Leslie include [468,191].
The Leslie consists primarily of a rotating horn and a rotating speaker port inside a wooden cabinet enclosure [189].
Rotating Horn Simulation
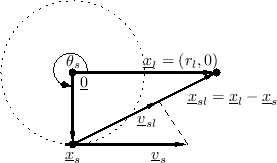
The heart of the Leslie effect is a rotating horn loudspeaker. The rotating horn from a Model 600 Leslie can be seen mounted on a microphone stand in Fig.5.7. Two horns are apparent, but one is a dummy, serving mainly to cancel the centrifugal force of the other during rotation. The Model 44W horn is identical to that of the Model 600, and evidently standard across all Leslie models [189]. For a circularly rotating horn, the source position can be approximated as
where
By Eq.
Note that the source velocity vector is always orthogonal to the source position vector, as indicated in Fig.5.8.
Since
![]() and
and
![]() are orthogonal,
the projected source velocity Eq.
are orthogonal,
the projected source velocity Eq.![]() (5.4) simplifies to
(5.4) simplifies to
Arbitrarily choosing
In the far field, this reduces simply to
Substituting into the Doppler expression Eq.
where the approximation is valid for small Doppler shifts. Thus, in the far field, a rotating horn causes an approximately sinusoidal multiplicative frequency shift, with the amplitude given by horn length
Rotating Woofer-Port and Cabinet
It is straightforward to extend the above computational model to include the rotating woofer port (``baffle'') and wooden cabinet enclosure as follows:
- In [189], it is mentioned that an AM ``throb'' is
the main effect of the rotating woofer port. A modulated
lowpass-filter cut-off frequency has been used for this purpose by
others. Measured data can be used to construct angle-dependent
filtering in a manner analogous to that of the rotating horn, and this
``woofer filter'' runs in parallel with the rotating horn model.
- The Leslie cabinet multiply-reflects the sound emanating from
the rotating horn. The first few early reflections are simply handled
as additional sources in Fig.5.6.
- To qualitatively simulate later, more reverberant
reflections in the Leslie cabinet, we may feed a portion of the
rotating-horn and speaker-port signals to separate states of an
artificial reverberator (see Chapter 3). This reverberator
may be configured as a ``very small room'' corresponding to the
dimensions and scattering characteristics of the Leslie cabinet, and
details of the response may be calibrated using measurements of the
impulse response of the Leslie cabinet. Finally, in order to emulate
the natural spatial diversity of a radiating Leslie cabinet in a room,
``virtual cabinet vent outputs'' can be extracted from the model and
fed into separate states of a room reverberator. An alternative
time-varying FIR filtering approach based on cabinet impulse-response
measurements over a range of horn angles is described in [191].
In summary, we may use multiple interpolating write-pointers to individually simulate the early cabinet reflections, and a ``Leslie cabinet'' reverberator for handling later reflections more statistically.
Recent Research Modeling the Leslie
As mentioned above, modeling the Leslie via interpolating delay-line writes and cabinet image-sources was described in [468].6.11More recently, Leslie simulation via time-varying FIR filtering has been developed [191]. See these papers and their cited references for further details.
Next Section:
Ideal Vibrating String
Previous Section:
Chorus Effect








![$\displaystyle \underline{x}_s(t) = \left[\begin{array}{c} r_s\cos(\omega_m t) \\ [2pt] r_s\sin(\omega_m t) \end{array}\right] \protect$](http://www.dsprelated.com/josimages_new/pasp/img1293.png)
![\includegraphics[width=4.1in]{eps/hornrecordingr}](http://www.dsprelated.com/josimages_new/pasp/img1296.png)
![$\displaystyle \underline{v}_s(t) = \frac{d}{dt}\underline{x}_s(t) = \left[\begi...
...in(\omega_m t) \\ [2pt] r_s\omega_m\cos(\omega_m t) \end{array}\right] \protect$](http://www.dsprelated.com/josimages_new/pasp/img1297.png)
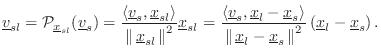
![$\displaystyle \underline{v}_{sl}= \frac{-r_l r_s\omega_m\sin(\omega_m t)}{r_l^2...
...l-r_s\cos(\omega_m t) \\ [2pt] -r_s\sin(\omega_m)t \end{array}\right]. \protect$](http://www.dsprelated.com/josimages_new/pasp/img1302.png)
![$\displaystyle \underline{v}_{sl}\approx -r_s\omega_m\sin(\omega_m t) \left[\begin{array}{c} 1 \\ [2pt] 0 \end{array}\right]. \protect$](http://www.dsprelated.com/josimages_new/pasp/img1303.png)











