DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Energy Decay Relief

The energy decay relief (EDR) is a time-frequency distribution which generalizes the EDC to multiple frequency bands [215]:

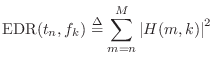
$\displaystyle \hbox{EDR}(t_n,f_k) \isdef \sum_{m=n}^M \left\vert H(m,k)\right\vert^2 $

where $ H(m,k)$ denotes bin $ k$ of the short-time Fourier transform (STFT) at time-frame $ m$ [12,451], and $ M$ denotes the total number of time frames. The FFT within the STFT is typically used with a window, such as a Hann window of length 30 or 40 ms.

Thus, $ \hbox{EDR}(t_n,f_k)$ is the total amount of signal energy remaining in the reverberator's impulse response at time $ t_n=nT$ in a frequency band centered about $ f_k=kf_s/N$ Hz, where $ N$ denotes the FFT length.

The EDR of a violin-body impulse response is shown in Fig.3.2. For better correspondence with audio perception, the frequency axis is warped to the Bark frequency scale [459], and energy is summed within each Bark band (one critical band of hearing equals one Bark). A violin body can be regarded as a very small reverberant room, with correspondingly ``magnified'' spectral structure relative to reverberant rooms.

Figure 3.2: Energy Decay Relief of a violin-body impulse response (from [203]).
\includegraphics[width=\twidth]{eps/bodyBEDR}

The EDR of the Boston Symphony Hall is displayed in [153, p. 96].

The EDR is used to measure partial overtone dampings from recordings of a vibrating string in §6.11.5.

Next Section:
Hadamard Matrix
Previous Section:
Energy Decay Curve