Free Books
   Free Books    Physical Audio Signal Processing  

EDR-Based Loop-Filter Design

This section discusses use of the Energy Decay Relief (EDR) (§3.2.2) to measure the decay times of the partial overtones in a recorded vibrating string.

First we derive what to expect in the case of a simplified string model along the lines discussed in §6.7 above. Assume we have the synthesis model of Fig.6.12, where now the loss factor $ g^N$ is replaced by the digital filter $ H_l(z)$ that we wish to design. Let $ \underline{x}(n)$ denote the contents of the delay line as a vector at time $ n$, with $ \underline{x}(0)$ denoting the initial contents of the delay line.

For simplicity, we define the EDR based on a length $ N$ DFT of the delay-line vector $ \underline{x}$, and use a rectangular window with a ``hop size'' of $ N$ samples, i.e.,

$\displaystyle \underline{X}_m(\omega_k) \isdef \dft _{N,\omega_k}\{\underline{x}_m\}, \quad m=0,1,2,\ldots, $

where $ \underline{x}_m(n)\isdef \underline{x}(mN)$. That is $ \underline{x}_m$ is simply the $ m$th successive snapshot of the delay-line contents, where the snapshots are taken once every $ N$ samples. We may interpret $ \underline{X}_m$ as $ m$th short-time spectrum of the output signal $ y^{+}(n)$ shown in Fig.6.12. Due to the special structure of our synthesis model, we have

$\displaystyle \underline{X}_m(\omega_k) = H_l^m(\omega_k) \underline{X}_0(\omega_k) $

for each DFT bin number $ k\in[0,N-1]$.

Applying the definition of the EDR (§3.2.2) to this short-time spectrum gives

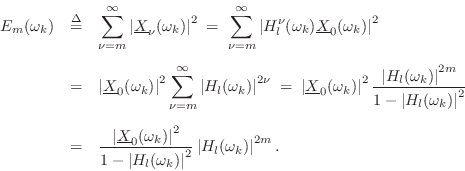
\begin{eqnarray*} E_m(\omega_k) &\isdef & \sum_{\nu=m}^\infty \left\vert\underl... ...omega_k)\right\vert^2} \left\vert H_l(\omega_k)\right\vert^{2m}. \end{eqnarray*}

We therefore have the following recursion for successive EDR time-slices:7.13

$\displaystyle E_{m+1}(\omega_k) = \left\vert H_l(\omega_k)\right\vert^2 E_m(\omega_k) $

Since we normally try to fit straight-line decays to the EDR on a log scale (typically a decibel scale), we will see the relation

$\displaystyle \log(E_{m+1}) = \log(E_m) + \log(\vert H_l\vert^2), $

where the common argument $ \omega_k$ is dropped for notational simplicity. Since we require $ \vert H_l(\omega_k)\vert<1$ for stability of the filtered-delay loop, the EDR decays monotonically in this example. Thus, the measured slope of the partial overtone decays will be found to be proportional to $ \log(\vert H_l\vert)$.

This analysis can be generalized to a time-varying model in which the loop filter $ H_l$ is allowed to change once per ``period'' $ N$.7.14

An online laboratory exercise covering the practical details of measuring overtone decay-times and designing a corresponding loop filter is given in [280].

Next Section:
Horizontal and Vertical Transverse Waves
Previous Section:
Fundamental Frequency Estimation