DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Equivalence of Series Combs to TDLs

It is also straightforward to show that a series combination of feedforward comb filters produces a sparsely tapped delay line as well. Considering the case of two sections, we have

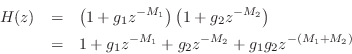
\begin{eqnarray*} H(z) &=& \left(1+g_1 z^{-M_1}\right) \left(1+g_2 z^{-M_2}\right)\\ &=& 1 + g_1 z^{-M_1} + g_2 z^{-M_2} + g_1 g_2 z^{-(M_1+M_2)} \end{eqnarray*}

which yields

$\displaystyle b_0 = 1,\; b_{M_1} = g_1,\; b_{M_2} = g_2,\; M_3=M_1+M_2,\;b_{M_3}=g_1 g_2. $

Thus, the TDL of Fig.2.19 is equivalent also to the series combination of two feedforward comb filters. Note that the same TDL structure results irrespective of the series ordering of the component comb filters.

Next Section:
Time Varying Comb Filters
Previous Section:
Equivalence of Parallel Combs to TDLs