Equivalence of Parallel Combs to TDLs
It is easy to show that the TDL of Fig.2.19 is equivalent to a
parallel combination of three feedforward comb filters, each as in
Fig.2.23. To see this, we simply add the three comb-filter transfer
functions of Eq.
(2.3) and equate coefficients:
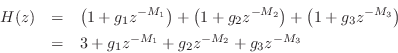
which implies
We see that parallel comb filters require more delay memory
(
elements) than the corresponding TDL, which only
requires
elements.
Next Section:
Equivalence of Series Combs to TDLs
Previous Section:
Filtered-Feedback Comb Filters
