FDN and State Space Descriptions
When
in Eq.
(2.10), the FDN (Fig.2.28)
reduces to a normal state-space model (§1.3.7),
The matrix
is the state transition matrix.
The vector
![$ \mathbf{x}(n) = [x_1(n), x_2(n), x_3(n)]^T$](http://www.dsprelated.com/josimages_new/pasp/img546.png){kind=small}
holds the state
variables that determine the state of the system at time 
. The
order of a state-space
system is equal to the number of state variables, i.e., the
dimensionality of
. The input and output signals have been
trivially redefined as
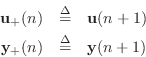
to follow normal convention for state-space form.
Thus, an FDN can be viewed as a generalized state-space model for a
class of 
th-order linear systems--``generalized'' in the sense
that unit delays are replaced by arbitrary delays. This
correspondence is valuable for analysis because tools for state-space
analysis are well known and included in many software libraries such
as with matlab.
Next Section:
Single-Input, Single-Output (SISO) FDN
Previous Section:
Time Varying Comb Filters
