DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Linear State Space Models

As introduced in Book II [449, Appendix G], in the linear, time-invariant case, a discrete-time state-space model looks like a vector first-order finite-difference model:

$\displaystyle \underline{y}(n)$ $\displaystyle =$ $\displaystyle C \underline{x}(n) + D\underline{u}(n)$  
$\displaystyle \underline{x}(n+1)$ $\displaystyle =$ $\displaystyle A \underline{x}(n) + B \underline{u}(n) \protect$ (2.8)

where $ \underline{x}(n)$ is the length $ N$ state vector at discrete time $ n$, $ \underline{u}(n)$ is in general a $ p\times 1$ vector of inputs, and $ \underline{y}(n)$ the $ q\times 1$ output vector. $ A$ is the $ N\times N$ state transition matrix, and it determines the dynamics of the system (its poles, or modal resonant frequencies and damping).

The state-space representation is especially powerful for multi-input, multi-output (MIMO) linear systems, and also for time-varying linear systems (in which case any or all of the matrices in Eq.$ \,$(1.8) may have time subscripts $ n$) [220].

To cast the previous force-driven mass example in state-space form, we may first observe that the state of the mass is specified by its velocity $ v(t)$ and position $ x(t)=\int v(t)\, dt$, or $ x[(n+1)T] = x(nT) + T\,v(nT)$.2.9Thus, to Eq.$ \,$(1.5) we may add the explicit difference equation

$\displaystyle x[(n+1)T] \eqsp x(nT) + T\,v(nT) \eqsp x(nT) + T\,v[(n-1)T] + \frac{T^2}{m} f[(n-1)T] $

which, in canonical state-space form, becomes (letting $ x_n\isdef x(nT)$, etc., for notational simplicity)

$\displaystyle \left[\begin{array}{c} x_{n+1} \\ [2pt] v_{n+1} \end{array}\right... ...ray}{c} 0 \\ [2pt] T/m \end{array}\right] f_n, \quad n=0,1,2,\ldots\,, \protect$ (2.9)

with $ x_0=v_0=0$ being a typical initial state.

General features of this example are that the entire physical state of the system is collected together into a single vector, and the elements of the $ (A,B,C,D)$ matrices include physical parameters (and the sampling interval, in the discrete-time case). The parameters may also vary with time (time-varying systems), or be functions of the state (nonlinear systems).

The general procedure for building a state-space model is to label all the state variables and collect them into a vector $ \underline{x}$, and then work out the state-transition matrix $ A$, input gains $ B$, output gains $ C$, and any direct coefficient $ D$. A state variable $ \underline{x}_i(n)$ is needed for each lumped energy-storage element (mass, spring, capacitor, inductor), and one for each sample of delay in sampled distributed systems. After that, various equivalent (but numerically preferable) forms can be generated by means of similarity transformations [449, pp. 360-374]. We will make sparing use of state-space models in this book, because they can be linear-algebra intensive, and therefore rarely used in practical real-time signal processing systems for music and audio effects. However, the state-space framework is an important general-purpose tool that should be kept in mind [220], and there is extensive support for state-space models in the matlab (``matrix laboratory'') language and its libraries. We will use it mainly as an analytical tool from time to time.

As noted earlier, a point mass only requires a first-order model:

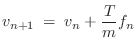
$\displaystyle v_{n+1} \eqsp v_n + \frac{T}{m} f_n $

Position $ x_n$ can always be computed from initial position $ x_0$ and velocity $ v_n$ by numerical integration:

$\displaystyle x_{n+1} \eqsp x_n + T\,v_n $

Impulse Response of State Space Models

As derived in Book II [449, Appendix G], the impulse response of the state-space model can be summarized as

$\displaystyle {\mathbf{h}}(n) \eqsp \left\{\begin{array}{ll} D, & n=0 \\ [5pt] CA^{n-1}B, & n>0 \\ \end{array} \right. \protect$ (2.10)

Thus, the $ n$th ``sample'' of the impulse response is given by $ C A^{n-1} B$ for $ n\geq0$. Each such ``sample'' is a $ p\times q$ matrix, in general.

In our force-driven-mass example, we have $ p=q=1$, $ B=[0,T/m]^T$, and $ D=0$. For a position output we have $ C=[1,0]$ while for a velocity output we would set $ C=[0,1]$. Choosing $ C=\mathbf{I}$ simply feeds the whole state vector to the output, which allows us to look at both simultaneously:

\begin{eqnarray*} {\mathbf{h}}(n+1) &=&\left[\begin{array}{cc} 1 & 0 \\ [2pt] 0 ... ...\left[\begin{array}{c} nT \\ [2pt] 1 \end{array}\right] \protect \end{eqnarray*}

Thus, when the input force is a unit pulse, which corresponds physically to imparting momentum $ T$ at time 0 (because the time-integral of force is momentum and the physical area under a unit sample is the sampling interval $ T$), we see that the velocity after time 0 is a constant $ v_n = T/m$, or $ m\,v_n=T$, as expected from conservation of momentum. If the velocity is constant, then the position must grow linearly, as we see that it does: $ x_{n+1} = n (T^2/m)$. The finite difference approximation to the time-derivative of $ x(t)$ now gives $ (x_{n+1}-x_n)/T = T/m = v_n$, for $ n\ge0$, which is consistent.

Zero-Input Response of State Space Models

The response of a state-space model Eq.$ \,$(1.8) to initial conditions, i.e., its initial state $ \underline{x}(0)$, is given by

$\displaystyle \underline{y}_x(n) \eqsp C A^{n-1}\underline{x}(0), \quad n=0,1,2,\ldots\,, $

and the complete response of a linear system is given by the sum of its forced response (such as the impulse response) and its initial-condition response.

In our force-driven mass example, with the external force set to zero, we have, from Eq.$ \,$(1.9) or Eq.$ \,$(1.11),

$\displaystyle \left[\begin{array}{c} x_{n+1} \\ [2pt] v_{n+1} \end{array}\right... ...ght] \eqsp \left[\begin{array}{c} x_0+v_0 n T \\ [2pt] v_0 \end{array}\right]. $

Thus, any initial velocity $ v_0$ remains unchanged, as physically expected. The initial position $ x_0$ remains unchanged if the initial velocity is zero. A nonzero initial velocity results in a linearly growing position, as physically expected. This response to initial conditions can be added to any forced response by superposition. The forced response may be computed as the convolution of the input driving force $ f_n$ with the impulse response Eq.$ \,$(1.11).

Next Section:
Transfer Functions
Previous Section:
State Space Models