DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Single-Input, Single-Output (SISO) FDN

When there is only one input signal $ u(n)$, the input vector $ \mathbf{u}(n)$ in Fig.2.28 can be defined as the scalar input $ u(n)$ times a vector of gains:

$\displaystyle \mathbf{u}(n) = \mathbf{B}u(n) $

where $ \mathbf{B}$ is an $ N\times 1$ matrix. Similarly, a single output can be created by taking an arbitrary linear combination of the $ N$ components of $ \mathbf{y}(n)$. An example single-input, single-output (SISO) FDN for $ N=3$ is shown in Fig.2.29.

Figure 2.29: Order 3 SISO Feedback Delay Network (FDN).
\includegraphics[width=\twidth]{eps/FDNSISO}

Note that when $ M_1=M_2=M_3=1$, this system is capable of realizing any transfer function of the form

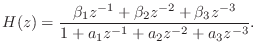
$\displaystyle H(z) = \frac{\beta_1z^{-1}+\beta_2z^{-2}+\beta_3z^{-3}}{1+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}}. $

By elementary state-space analysis [449, Appendix E], the transfer function can be written in terms of the FDN system parameters as

$\displaystyle H(z) = \mathbf{C}^T(z\mathbf{I}- \mathbf{A})^{-1}\mathbf{B} $

where $ \mathbf{I}$ denotes the $ 3\times 3$ identity matrix. This is easy to show by taking the z transform of the impulse response of the system.

The more general case shown in Fig.2.29 can be handled in one of two ways: (1) the matrices $ \mathbf{A}, \mathbf{B}, \mathbf{C}$ can be augmented to order $ N=M_1+M_2+M_3$ such that the three delay lines are replaced by $ N$ unit-sample delays, or (2) ordinary state-space analysis may be generalized to non-unit delays, yielding

$\displaystyle H(z) = \mathbf{C}^T \mathbf{D}(z)\left[\mathbf{I}- \mathbf{A}\mathbf{D}(z)\right]^{-1}\mathbf{B} $

where $ \mathbf{C}^T$ denotes the matrix transpose of $ \mathbf{C}$, and

$\displaystyle \mathbf{D}(z) \isdef \left[\begin{array}{ccc} z^{-M_1} & 0 & 0\\ [2pt] 0 & z^{-M_2} & 0\\ [2pt] 0 & 0 & z^{-M_3} \end{array}\right]. \protect$

In FDN reverberation applications, $ \mathbf{A}={\bm \Gamma}\mathbf{Q}$, where $ \mathbf{Q}$ is an orthogonal matrix, for reasons addressed below, and $ {\bm \Gamma}$ is a diagonal matrix of lowpass filters, each having gain bounded by 1. In certain applications, the subset of orthogonal matrices known as circulant matrices have advantages [385].

Next Section:
FDN Stability
Previous Section:
FDN and State Space Descriptions